Week of 1/21/08
From Physiki
(Difference between revisions)
(New page: [http://mathworld.wolfram.com/HermitianInnerProduct.html Definition of complex (Hermitian) inner product] <math><u+v,w>==<u,w>+<v,w></math> <math><u,v+w>==<u,v>+<u,w></math> <math><\alp...) |
|||
| (19 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
[http://mathworld.wolfram.com/HermitianInnerProduct.html Definition of complex (Hermitian) inner product] | [http://mathworld.wolfram.com/HermitianInnerProduct.html Definition of complex (Hermitian) inner product] | ||
| − | |||
| − | + | It's a matter of convention that the anti-linear term is the second one in the inner product: | |
| − | <math> | + | <math> \langle u+v,w \rangle \equiv \langle u,w \rangle + \langle v,w \rangle </math> |
| − | <math> | + | <math> \langle u,v+w \rangle \equiv \langle u,v \rangle + \langle u,w \rangle </math> |
| − | <math> | + | <math> \langle \alpha u,v \rangle \equiv \alpha \langle u,v \rangle </math> |
| − | <math> <u,u>>=0,</math> with equality only if <math>u | + | <math> \langle u,\alpha v \rangle \equiv \alpha^* \langle u,v \rangle </math> |
| + | |||
| + | <math> \langle u,v \rangle \equiv \langle v,u \rangle ^* </math> | ||
| + | |||
| + | <math> \langle u,u \rangle = 0, </math> with equality only if <math>u \equiv 0</math> | ||
The basic example is the form | The basic example is the form | ||
| − | <math>h(z,w) | + | <math>h(z,w) \equiv \sum z_i w^* _i</math> |
| + | |||
| + | However, Griffiths uses a different convention with the complex conjugate on the first term: cf page 94. So, I will change mine to conform to his. | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | '''NB''' if <math>z = x + I y</math>, then <math>z^* z = (x - I y)(x + I y) = x^2 + y^2 = z z^*</math> | ||
| + | |||
| + | |||
| + | {{Mathematica|filename=Superposition.nb|title=Animation of the superposition of two eigenstates for a 1D string}} | ||
| + | |||
| + | |||
| + | {{PDF|filename=1-21-08.pdf|title=Lecture notes 1/21/08. Sep. of Variables of TDSE. Eigenstates. Stationary states.}} | ||
| + | |||
| + | |||
| + | {{PDF|filename=1-23-08.pdf|title=Lecture notes 1/23/08. Review of Hermitian matrices/operators. Particle in an infinite square well.}} | ||
| + | |||
| + | |||
| + | {{Mathematica|filename=Particleinbox.nb|title=evolution of a gaussian particle in a box}} | ||
| + | |||
| + | |||
| + | {{Mathematica|filename=Griffiths_example2.2.nb|title=Mathematica version of Griffiths analytic example 2.2}} | ||
| + | |||
| + | {{PDF|filename=1-25-08.pdf|title=Lecture notes 1/25/08. Review of integration by parts. Stationary states. Fourier superposition. Completeness and orthogonality of eigencuntions of Hermitian operators. Example 2.2 in book. Quantum harmonic oscillator}} | ||
| + | |||
| + | |||
| + | [http://eve.physics.ox.ac.uk/Personal/artur/Keble/Quanta/Applets/quantum/deepwellmain.html very nice applet illustrating the dynamics of a deep well] | ||
Latest revision as of 17:53, 25 January 2008
Definition of complex (Hermitian) inner product
It's a matter of convention that the anti-linear term is the second one in the inner product:
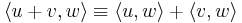
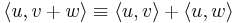
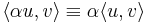
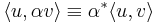
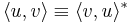
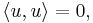with equality only if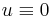 
The basic example is the form
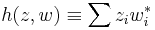
However, Griffiths uses a different convention with the complex conjugate on the first term: cf page 94. So, I will change mine to conform to his.
NB if z = x + Iy, then z * z = (x − Iy)(x + Iy) = x2 + y2 = zz *
 Download Animation of the superposition of two eigenstates for a 1D string
|
 Download Lecture notes 1/21/08. Sep. of Variables of TDSE. Eigenstates. Stationary states.
|
| Download Lecture notes 1/23/08. Review of Hermitian matrices/operators. Particle in an infinite square well.
|
| Download evolution of a gaussian particle in a box
|
| Download Mathematica version of Griffiths analytic example 2.2
|
