Stable Manifold Theorem
From Physiki
(Difference between revisions)
(New page: {{Start Hierarchy|link=Main Page|title=Main Page}} {{Hierarchy Item|link=Bill:Lee|title=Bill:Lee}} {{Hierarchy Item|link=Mathematics|title=Mathematics}} {{End Hierarchy}} Let $E$ be an op...) |
|||
| (One intermediate revision by one user not shown) | |||
| Line 4: | Line 4: | ||
{{End Hierarchy}} | {{End Hierarchy}} | ||
| − | Let | + | Let <math>E</math> be an open subset of <math>\mathbb{R}^{n}</math>, which contains the origin, let <math>\textbf{f}\in C^{1}(E)</math>, and let <math>\phi_{t} </math> be the flow of the nonliear system <math>\dot{\textbf{x}} = \textbf{f}(\textbf{x})</math>. Suppose <math>\textbf{f}(\textbf{0})=\textbf{0}</math> and that <math>D\textbf{f}(\textbf{0})</math> has <math>k</math> eigenvalues with negative real part and <math>n-k</math> eigenvalues with positive real part. Then there exists a <math>k-</math>dimensional differentiable manifold <math>S</math> tangent to the sable subspace <math>E^{s}</math> of the linear system <math>\dot{\textbf{x}} =\textbf{Ax}</math> at <math>\textbf{0}</math>such that for all <math>t\geq 0</math>, <math>\phi_{t}(S) \sub S</math> and for all <math>\textbf{x}_{0} \in S</math>, <math>\lim_{t\to\infty} \phi_{t}(\textbf{x}_{0}) = \textbf{0}</math>; and there exists an <math>n-k</math> dimensional differentiable manifold <math>U</math> tangent to the unstable subspace <math>E^{u}</math>of the linear system at <math>\textbf{0}</math> such that for all <math>t\leq 0</math>, <math>\phi_{t}(U)\sub U</math> and for all <math>\textbf{x}_{0}\in U</math>, <math>\lim_{t\to -\infty} \phi_{t}(\textbf{x}_{0})=\textbf{0}</math> |
| − | + | ||
| − | + | ||
| − | + | ==References== | |
| − | + | [http://books.google.com/books?id=A7fvvz9Puf8C&dq=differential+equations+and+dynamical+systems+perko&pg=PP1&ots=_DkccInx4B&sig=K27_M_77UOxgOjIJp41B-zz__4I&hl=en&prev=http://www.google.com/search%3Fhl%3Den%26client%3Dsafari%26rls%3Den%26q%3Ddifferential%2Bequations%2Band%2Bdynamical%2Bsystems%2BPerko%26btnG%3DSearch&sa=X&oi=print&ct=title&cad=one-book-with-thumbnail Differential Equations and Dynamical Systems] : Lawrence Perko, page 109, theorem 2, third edition | |
| − | + | ||
| − | and | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 03:56, 28 May 2008
| Main Page | > | Bill:Lee | > | Mathematics |
Let E be an open subset of 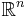 , which contains the origin, let
, which contains the origin, let 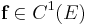 , and let φt be the flow of the nonliear system
, and let φt be the flow of the nonliear system  . Suppose
. Suppose 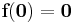 and that
and that 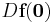 has k eigenvalues with negative real part and n − k eigenvalues with positive real part. Then there exists a k − dimensional differentiable manifold S tangent to the sable subspace Es of the linear system
has k eigenvalues with negative real part and n − k eigenvalues with positive real part. Then there exists a k − dimensional differentiable manifold S tangent to the sable subspace Es of the linear system 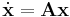 at
at 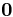 such that for all
such that for all 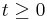 ,
, 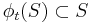 and for all
and for all 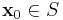 ,
, 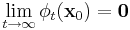 ; and there exists an n − k dimensional differentiable manifold U tangent to the unstable subspace Euof the linear system at
; and there exists an n − k dimensional differentiable manifold U tangent to the unstable subspace Euof the linear system at 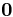 such that for all
such that for all 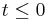 ,
, 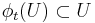 and for all
and for all 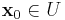 ,
, 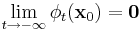
References
Differential Equations and Dynamical Systems : Lawrence Perko, page 109, theorem 2, third edition