Stable Manifold Theorem

Main Page

>

Bill:Lee

>

Mathematics

Let E be an open subset of 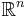$\mathbb{R}^{n}$, which contains the origin, let 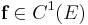$\textbf{f}\in C^{1}(E)$, and let φ_t be the flow of the nonliear system 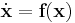$\dot{\textbf{x}} = \textbf{f}(\textbf{x})$. Suppose 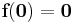$\textbf{f}(\textbf{0})=\textbf{0}$ and that 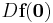$D\textbf{f}(\textbf{0})$ has k eigenvalues with negative real part and n − k eigenvalues with positive real part. 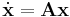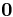Then there exists a k − dimensional differentiable manifold S tangent to the sable subspace E^s of the linear system $\dot{\textbf{x}} =\textbf{Ax}$ at $\textbf{0}$such that for all 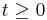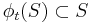$t\geq 0$, $\phi_{t}(S) \sub S$ and for all 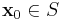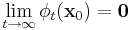$\textbf{x}_{0} \in S$, $\lim_{t\to\infty} \phi_{t}(\textbf{x}_{0}) = \textbf{0}$; and there exists an n − k dimensional differentiable manifold U tangent to the unstable subspace E^uof the linear system at 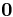$\textbf{0}$ such that for all 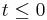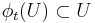$t\leq 0$, $\phi_{t}(U)\sub U$ and for all $\textbf{x}_{0}\in U$, $\lim_{t\to -\infty} \phi_{t}(\textbf{x}_{0})=\textbf{0}$

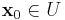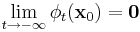
References

Differential Equations and Dynamical Systems : Lawrence Perko, page 109, theorem 2, third edition