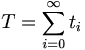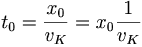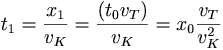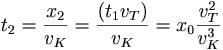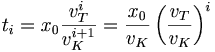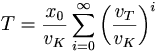Problem 4:Catching a turtle

It is impossible for me to catch a turtle. To prove it let the turtle be a distace D0 away from me at t=0. Also let the turtle move at constant speed v away from me while I travel at constant speed V toward the turtle. By the time I reach the place where the turtle was at t=0, the turtle has moved forward to a distance D1. By the time I reach D1 the turtle has moved to D2. This process continues forever and I therefore will never reach the turtle.

This is not necessarily true. If your speed, V, is larger in magnitude than the turtle's speed, v, then D0, D1, D2, D3, etc will keep getting smaller. Eventually you will be able to reach the turtle and overtake him if you want to.

If your speed, V, is the same in magnitude as the turtle's speed, v, then the statement is correct, you will never reach the turtle. However, D0, D1, D2, D3, etc will all be the same distance, and the turtle will remain a constant distance from you.

If your speed, V, is smaller in magnitude than the turtle's speed, v, then the statement is not still correct. You will never reach the turtle. However, D0, D1, D2, D3, etc will keep increasing in distance and the turtle will keep going faster than you. Since the turtle keeps increasing his distance from you, you will chase the turtle around the world and eventually he will catch up to you. When this happens then you can grab him. However this does assume that you can run in a straight line around the world, it may not be possible right now, but I will complete the neccessary roads to do this shortly.

Mathematically, this series will converge to zero over an infinite amount of terms assuming that Dr. Kowalski's speed is greater than the turtle's speed. This means that the distance between you and the turtle will keep getting smaller and smaller and eventually, you will be able to reach out and grab the turtle. This means that, depending on the initial speeds of the turtle and Professor Kowalski, the initial statement is not necessarily true.

In order to show this mathematically, we assume that Dr. Kowalski can run at a velocity of v_K and the turtle walks at v_T. We will assume that both of them run in a straight line, to stay away from any annoying trigonometry. The time for Dr. Kowalski to reach the initial position of the turtle (x₀) is t₀ = x₀ / v_K. By then, the turtle has moved a distance of x₁ = t₀v_T. It then takes t₁ = x₁ / v_K for Dr. Kowalski to get there, and so on. This implies that, if T is the time it takes to catch the turtle:

$T = \sum_{i=0}^{\infty} t_i$

Where

$t_0 = \frac{x_0}{v_K}=x_0\frac{1}{v_K}$

$t_1 = \frac{x_1}{v_K} = \frac{(t_0 v_T)}{v_K}=x_0 \frac{v_T}{v^2_K}$

$t_2 = \frac{x_2}{v_K} = \frac{(t_1v_T)}{v_K} =x_0 \frac{v^2_T}{v^3_K}$

$\vdots$

$t_i = x_0\frac{v^{i}_T}{v^{i+1}_K} = \frac{x_0}{v_K}\left(\frac{v_T}{v_K}\right)^i$

So, we finally get for time T:

$T = \frac{x_0}{v_K}\sum_{i=0}^{\infty} \left(\frac{v_T}{v_K}\right)^i$

Which is a geometric series that converges to x₀ / (v_K − v_T) if v_T / v_K is less than 1, as expected by natural intuition.

Not to sound redundant but this is similar to how 9/9 is both 0.9 repeating but also it converges to 1.