Problem 3:Vacuum Diode

In a vacuum diode, electrons are "boiled" off a hot cathode, at potential zero, and accelerated across a gap to the anode, which is held at positive potential V_o. The cloud of moving electrons within the gap (called space charge) quickly builds up to the point where it reduces the field at the surface of the cathode to zero. From then on a steady current I flows between the plates. Suppose the plates are large relative to the separation (A >> d^2 where A is the area and d the plate separation), so that edge effects can be neglected. Then, V_o, ρ (charge density), and v (electron speed) are all functions of x alone.

(a) What is Poisson's equation in the region between the plates?

$\nabla^2V=\frac{\rho(x)}{\epsilon_o}$

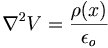
(b) Assuming the electrons start from rest at the cathode, what is their speed at point x, where the potential is V(x)?

By conservation of energy, the velocity must satisfy:

$\frac{1}{2}m v^2(x)-V(x)=0$

$v(x) = \sqrt{\frac{2 V(x)}{m}}$

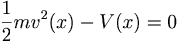
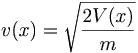
(c) In the steady state, I is independent of x. What, then, is the relation between ρ and v?

$\rho v = \frac{I}{A}$

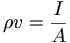
where A is the area of the plate. This is a guess, but it works out units wise, and it makes sense. I'm confident ρv is constant, but I'm just not positive which constant...

(d) Use these results to obtain a differential equation for B, by eliminating rho and v.

(e) Solve this equation for V as a function of x, V0,, and d. What does V(x) look like and what does it look like without space-charge?

Without the space-charge it is the homogeneous equation:

$\frac{d^2V}{dx^2} = 0$

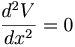
Solution with boundary conditions:

$V(x) = \frac{V_0}{d}x$

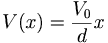
If you consider the differential equation with the forcing effect of rho, which was given in as a function of velocity, where velocity was also given as a function of potential, you obtain the following differential equation:

$\nabla^2V=\frac{I}{A \epsilon_0} \sqrt{\frac{m}{2 V(x)}}$

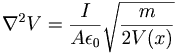
To find the solution I put the terms involving v on one side and the constants and the dx on the other and integrated twice, maintaining a constant each time on the x side. This led to the general solution:

$V^{5/2} = \frac{15}{4}(\frac{K x^2}{2} + Cx + D)$ where $K = \frac{I \sqrt{m}}{A \epsilon_o \sqrt{2}}$

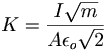
Applying the boundary conditions that V go to 0 at x = 0 and V go to V₀ when x = d gives

$V(x) = (\frac{15}{4}(\frac{I \sqrt{m}x^2}{A \epsilon_o \sqrt{2}} + (\frac{4 V_0^{5/2}}{15 d}- \frac{I \sqrt{m}d}{A \epsilon_o 2\sqrt{2}})x))^{2/5}$

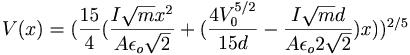
I don't think this is right but it may be close becuase it almost derives the result listed in part g only the power of V0 seems wrong.

(f) Find rho and v as a function of x.

(g) How can you derive the result I = K V0^(-3/2)? What is the constant K?