PHGN-471 Fall-2011
| Main Page | > | Physics Course Wikis |
Contents
|
Course Information
Instructor: Eric Toberer
Research Assistant: Aaron Martinez
Students: Kyle Conrad and Michael Dixon
Project Title: Predicting the behavior of thermoelectric materials via the Boltzmann transport equation
Objective
Understanding electronic transport in semiconductors materials is critical for the development of advanced thermoelectric materials of energy harvesting. To date, modeling thermoelectric materials typically involves applying solutions to the Boltzmann transport equation within the limit of a single parabolic band. This senior design project will consider the effect of non parabolic bands, multiple bands, and inter-band scattering on the predicted properties of thermoelectric materials.
The goal of this project is to use the advanced transport expressions to determine an optimal thermoelectric band structure and develop guidelines for the selection of thermoelectric materials.
Transport Theory
Density of States
Now the system of N free electrons in occupied orbitals can be represented by points in a sphere in k-space. At absolute zero, the wave vector representing the radius of the sphere corresponds to the fermi energy. Each point corresponds to a distinct set of quantum numbers for a volume element (2π / L)3 in k-space. The total number of occupied orbitals in k-space.

or,

Putting equation 1.18 into equation 1.16 gives,

Solving this equation for N and differentiating with respect to E gives an expression for the number of orbitals per unit energy. This quantity is called the density of states.

This expression can be thought of as the quotient of the number of conduction electrons and the fermi energy.
The density of electrons at zero temperature is given by:

The limits on your integral are from zero to the fermi energy. We con do the same thing for nonzero temperatures by multiplying by the fermi-dirac distribution. From this the low-temperature heat capacity of a fermi gas can be determined. (Kittel pg 100)
Distribution Functions
Distribution functions are functions that have little importance on their own, but when integrated form a meaningful value, like a probability. Three distribution functions will be examined; the Maxwell distribution, the Fermi-Dirac distribution, and the Bose-Einstein distribution.
Boltzmann Distribution
Consider a system of noninteracting particles. The Boltzmann distribution gives the probability of finding this system in a particular energy state, E, at temperature, T.\\ Suppose this system has two possible localized energy states E1andE2. The probability these two states occurring at the same time is given by:
P1,2 = P1 * P2
and the total energy of the system is given by:
E1,2 = E1 + E2
From this it can be concluded that the probability of the system being in a particular energy state must be an exponential function.

where,

kB is the Boltzmann constant and has been determined experimentally to be 1.381 * 10 − 23J / K. The Boltzmann distribution can now be written as:

$P_{r}$ gives the probability of finding the system in state r with energy Er at temperature T. Normalizing such that \[\sum_{r}P_{r}=1\] gives:

where Z is called the partition function.
Partition Function
Quote from Lindsay:
\textit{Once a partition function is calculated, all other equilibrium thermodynamic properties follow from minimizing the free energy of the system expressed in terms of the partition function}
The grand partition function is given by:

where $\mu$ is the chemical potential and Nr is the number of particles in a particular state.
Maxwell Distribution
Begin by considering an ideal gas. We will want to consider the motions of an individual molecule within the gas. More specifically, we will ask the question "What is the probability of a particular molecule moving at a given speed?". There are infinitely many speeds that the molecule may travel at, so the probability of the speed being a particular one is nearly zero. But relative to each other, some speeds are more probable than others so the relative probability of each speed must be considered. A plot of the relative probability for each speed v is shown below. This graph is normalized (the area underneath the curve is 1) so the area between two speeds is the probability that a molecule's speed is within the specified range.
INSERT GRAPH OF D(V)
The graph shows D(v), but what is D(v)? The equation below describes the two factors in the equation

The probability of a molecule having 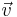 is given by the Boltzmann Factor,
is given by the Boltzmann Factor,  . In the ideal gas, the total energy is due purely to the kinetic so
. In the ideal gas, the total energy is due purely to the kinetic so  The second factor in the equation can be found by considering 3 dimensional velocity space. In this space, the number of vectors
The second factor in the equation can be found by considering 3 dimensional velocity space. In this space, the number of vectors 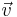 corresponding to v is the surface of a sphere of radius v.
corresponding to v is the surface of a sphere of radius v.
Surface Area = 4πv2
D(v) is normalized, so the surface area, the Boltzmann factor, and a normalizing constant must be integrated from 0 to infinity and set equal to 1. Solving this for the normalizing constant completes Maxwell's distribution.

Fermi-Dirac and Bose-Einstein Distributions
Consider a system of indistinguishable particles with only one particle state. The energy of the particle is defined as follows: ε when occupied, 0 when empty, and nε when occupied by n particles. The probability of a state being occupied by n particles is given by
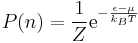
where Z is the grand partition function, μ is the chemical potential, and T is the temperature. Occupancy is the average number of particles in a state, and for this system is
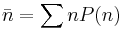
Because fermions can not have the same set of quantum numbers as each other (Pauli Exclusion Principle) n can only be 1 or 0. As well the partition function for fermions is
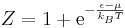
This generates the Fermi-Dirac distribution

Independent, Free Electron Gas
- Conduction electron move freely through the volume of the metal. Valence electrons and nuclei are fixed in place
- Correctly predicts Ohm's law and electrical-thermal conductivity relation
- Cannot explain heat capacity or magnetic susceptibilities of conduction electrons
Two important notes:
- Ion cores do not scatter conduction electrons is the cores form periodic potential. This is because matter waves propagate freely in a periodic structure. (See chapter 7 of Kittel)
- Electron-electron scattering is infrequent. (Consequence of Pauli exclusion)
Failures of this model:
- Predicts a significant heat capacity from electrons
- Does not account for variation of resistivity with temperature
- Cannot explain why electron free path is so great
Energy Bands
Energy gaps cannot be derived from the free electron model. It can only be accomplished via the examination of the electron wave functions. k-values that satisfy the Bragg reflection condition create standing waves. These standing waves aggregate charge at different values of potential energy. This introduces the concept of an energy gap.
Fermi Energy
Consider a Fermi gas of N electrons at absolute zero. When considering spin  , two electrons can be in any one orbital. The energy level of the most energetic electron of this system is termed the Fermi energy εf. It is only electrons located near the fermi energy that contribute to transport. This is because electrons move from state to state in steps of no more than kBT.
, two electrons can be in any one orbital. The energy level of the most energetic electron of this system is termed the Fermi energy εf. It is only electrons located near the fermi energy that contribute to transport. This is because electrons move from state to state in steps of no more than kBT.
Boltzmann Transport
Electrical Current
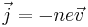
Thermal Current
Transport Coefficients
Electrical Conductivity
Thermal Conductivity
Seebeck
An understanding of this quantity should begin with a discussion of the seebeck coefficient. The seebeck effect describes the creation of a voltage across a material in response to a temperature gradient. The ratio of the voltage drop induced to the temperature gradient is a property intrinsic to a material and termed the seebeck coeficient.

Peltier
This process is analogous to the seebeck effect. Some materials will absorb heat when a current is passed through it. The peltier coefficient can be defined as the ratio of the heat carried by the charges to the current across the material.
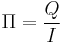
The peltier coefficient can also be related to the seebeck coefficient:
Π = αT
Hall
Consider a substance carrying a current in the x-direction with a magnetic field applied in the z-direction. An E-field will occur in the y-direction and is called the Hall field. The Hall field will be proportional to the product of the current density and the magnitude of the applied magnetic field. The constant of proportionality is the Hall Coefficient. EH = − RJH. The Hall effect allows for the determination of carrier concentration and mobility. The Hall effect can be explained from a semi-classical standpoint.
Nernst
Consider a sample with a thermal current in the x-direction and a magnetic field in the z-direction. An electric field will be induced in the y-direction.
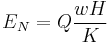
Where Q is the Nernst coefficient, w is the thermal current, H is the magnetic field perpendicular to current flow, and K is the thermal conductivity of the sample.
Ettingshausen
Consider a sample with a current flow in the x-direction and an applied electric field in the z-direction. If this occurs a temperature gradient will appear in y-direction.
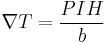
Where P is the Ettingshausen coefficient, I is the current, H is the magnetic field perpendicular to current flow, and b is the thickness of the sample.
Righi-Leduc
References
- Thermal Physics, Daniel V. Schroeder. 2000
- Solid State Physics, Charles Kittel. 2005
- Introduction to Quantum Mechanics, David Griffiths.
- Condensed Matter in a Nutshell, Gerald Mahan.
- Introduction to Nanoscience, S.M. Lindsay.
- Thermoelectrics: Basic Principles and New Materials Developments, G.S. Nolas
- Solid State Physics, Ashcroft and Mermin. 1976