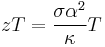PHGN-471 Fall-2011
| Main Page | > | Physics Course Wikis |
Contents |
Modeling Transport in Thermoelectric Materials
Advisor: Eric Toberer
Graduate Advisor: Aaron Martinez
Students: Kyle Conrad and Michael Dixon
Objective
Thermoelectric materials generate electricity from waste heat. Understanding electronic transport in semiconductors materials is critical for the development of a new generation of thermoelectric devices. These materials could potentially play a role in the world's future energy infrastructure. To date, modeling thermoelectric materials typically involves applying solutions to the Boltzmann transport equation within the limit of a single parabolic band. This senior design project will consider transport beyond the parabolic band assumption. The goal of this project is to use advanced transport expressions to determine an optimal thermoelectric band structure and develop guidelines for the selection of thermoelectric materials. The goal of this wiki page is to serve as a record of the material covered over the course of the year as well as assist others who are curious about the exciting and dynamic field of semiconductor transport and thermoelectric materials.
The ideal procedure is as follows:
Compound of Interest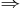 Crystal Structure
Crystal Structure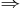 Band Structure
Band Structure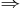 Transport Properties
Transport Properties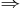 Figure of Merit
Figure of Merit
This project is concerned with the latter half of this track. That is, we want to be able to take any band structure and be able to supply a reliable prediction of its thermoelectric figure of merit.
Introductory Concepts
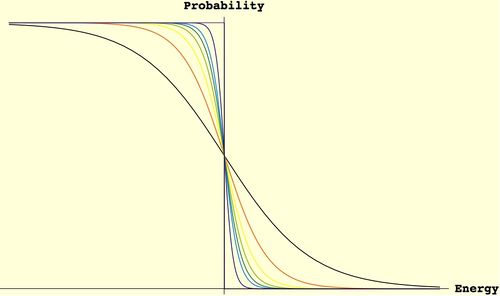
Fermi-Dirac Distribution
[1]The Fermi-Dirac distribution is integral to the theory of transport and is briefly examined here. Consider a system of indistinguishable particles with only one particle state. The energy of the particle is defined as follows: ε when occupied, 0 when empty, and nε when occupied by n particles. The probability of a state being occupied by n particles is given by
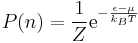
where Z is the grand partition function, μ is the chemical potential, and T is the temperature. Occupancy is the average number of particles in a state, and for this system is
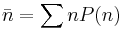
Because fermions can not have the same set of quantum numbers as each other (Pauli Exclusion Principle) n can only be 1 or 0. The partition function for fermions is
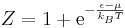
This generates the Fermi-Dirac distribution
Fermi Energy
Consider a Fermi gas of N electrons at absolute zero. When considering spin 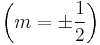 , two electrons can be in any one orbital. The energy level of the most energetic electron of this system is termed the Fermi energy εf. It is only electrons located near the fermi energy that contribute to transport. This is because electrons move from state to state in steps of no more than kBT. Where kB is Boltzmann's constant
, two electrons can be in any one orbital. The energy level of the most energetic electron of this system is termed the Fermi energy εf. It is only electrons located near the fermi energy that contribute to transport. This is because electrons move from state to state in steps of no more than kBT. Where kB is Boltzmann's constant
Wave vector Space
Possible electron quantum states can be represented in a three dimensional wave vector space. Any point in this space corresponds to the three quantum numbers kx,ky,kz. Recall that the wave vector k is related to the mean electron momentum by
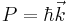
Although the states are quantized they can be treated as continuous.
Density of States
The density of states is an incredibly important quantity not only in the study of transport but in statistical mechanics in general. Put simply the density of states is a measure of the number of available states per interval of energy. We've seen that possible states can be represented with a wave vector k.
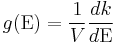
Chemical and Electrochemical Potential
[2]Consider a system of N particles held at T=0. In this case the only change in energy can come from a change in free energy or by allowing the system to exchange particles with the surroundings. Under these conditions the change in energy can be written as:
dE = dF + μdN
If we impose an additional condition that there is no change in energy than the quantity μ, termed the chemical potential is defined as:
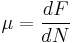
Therefore, the chemical potential can be interpreted as the amount of energy changed given a change in the number of particles. If we now adjust our expression to include the change in the amount of charge we have:
dE = dF + μdN + ψdq
where \psi is the electrostatic potential 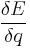 . Since dq = edN the above expression can be written as:
. Since dq = edN the above expression can be written as:
dE = dF + (μ − eψ)dN
The quantity in front of dN is known as the electrochemical potential and is typically also denoted using μ
Modeling Materials
Drude Model
Drude's model is constructed by applying the kinetic theory of gases to metals. In the kinetic theory of ideal gases molecules are assumed to be identical solid spheres which move in straight lines until a collision occurs.[3] It is assumed that when metallic elements come together to form a lattice, the weakly bound valence electrons become delocalized and move freely, while the positively charged ions and core electrons are assumed fixed in place. Ultimately the motion of electrons is given by the following: (mahan 322)
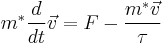
Where 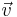 is the electron velocity, m * is the effective mass, τ is the relaxation time, and F is the force determined by the Lorentz force law. Another valuable result of this model is the Drude formula, which describes electrical conductivity as a function of frequency.
is the electron velocity, m * is the effective mass, τ is the relaxation time, and F is the force determined by the Lorentz force law. Another valuable result of this model is the Drude formula, which describes electrical conductivity as a function of frequency.
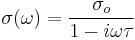
with
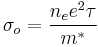
The assumptions that go into the Drude model are as follows. Electron-electron interactions are ignored and electrons interact with ions only through collisions. These two assumptions are widely known as the independent electron approximation, and free electron approximation respectively. The independent electron approximation, although seemingly brash, can be defended. Electron-electron scattering is infrequent as a consequence of the Pauli exclusion principle. An electron can only scatter into an already unoccupied state. As we move to more advanced models of electron transport, the free electron approximation will be quickly abandoned. Next, we assume the existence of a relaxation time τ. To do this, it is assumed that the probability of an electron sucumbing to a scatterin event is 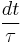 . The relaxation time is the average time that an electron will travel without experiencing a collision. Also, it is assumed that scattering events is the only manner in which electrons can reach thermal equilibrium. After the collision the electron is emitted with a random direction and a speed which is dependent on the temperature where the collision occurred. We will see later that the relaxation time depends on other quantities and cannot be taken as constant. As basic as this model is, it does allow for calculation of the electrical and thermal conductivity as well as the hall coefficient. Perhaps the biggest failure of the Drude model is that it does not allow for a distinction between metals, semiconductors, and insulators.
. The relaxation time is the average time that an electron will travel without experiencing a collision. Also, it is assumed that scattering events is the only manner in which electrons can reach thermal equilibrium. After the collision the electron is emitted with a random direction and a speed which is dependent on the temperature where the collision occurred. We will see later that the relaxation time depends on other quantities and cannot be taken as constant. As basic as this model is, it does allow for calculation of the electrical and thermal conductivity as well as the hall coefficient. Perhaps the biggest failure of the Drude model is that it does not allow for a distinction between metals, semiconductors, and insulators.
Sommerfeld Model of a Crystal
The inception of quantum theory brought about some alterations to the Drude model. Put simply, the Sommerfeld model is the Drude model with the modification that the velocity distribution is taken as the quantum based Fermi-Dirac distribution as opposed to the Maxwell-Boltzmann distribution. The solution to the Schrodinger equation characterized available quantum states and the Fermi-Dirac distribution determines how the states are populated.
Quantum treatment of free Electron Transport and Origin of Effective Mass
(Askerov Chapter 1)

and the wavefunction takes the form

Thus we can obtain a relationship between energy and wave vector
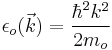
A more proper analysis includes also the coulomb interaction between the electrons and the periodic potential of the ions. In this case Schrodinger's equation looks like
![\left[\left(\frac{-\hbar^{2}}{2m_{o}}\right)\nabla^{2}+ V(\vec{r})\right]\psi_{\vec{k}}(\vec{r}) = \epsilon_{o}(\vec{k})\psi_{\vec{k}}(\vec{r})](/csm/wiki/images/math/e/a/9/ea96923c3845acfae4127fa88f94926d.png)
Assuming the Bloch wave function
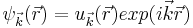
Then the group velocity will contain the term
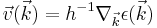
Now since 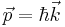 and force is equal to the time derivative of momentum, an effective mass tensor can be constructed to relate the acceleration and force components
and force is equal to the time derivative of momentum, an effective mass tensor can be constructed to relate the acceleration and force components
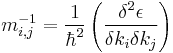
where i and j correspond to x, y, z. Note that the effective mass is proportional to the curvature of the fermi surface.
Semiconductors
Nearly Free Electron Model and the Origin of Energy Gaps
Energy gaps cannot be derived from the free electron model. They arise only when we allow electrons to be weakly perturbed by the ion potential (nearly free electron model). Wavevector values that satisfy the Bragg reflection condition create standing waves. These standing waves result in an aggregation of charge on the ion core and in between the cores. These two locations have a different value of potential energy and result in a gap of forbidden energies that is equal to twice the fourier component of the potential. This is described in more detail in this link. [1]
Formally, the dispersion relation can be written in the following form (Askerov Chapter 1)
![\epsilon_{1,2}(\vec{k}) = \frac{1}{2}[\epsilon_o(\vec{k}) + \epsilon_{o}(\vec{k} + \vec{b}_{g})] \pm \frac{1}{2}\sqrt{[\epsilon_o(\vec{k}) - \epsilon_{o}(\vec{k} + \vec{b}_{g})]^{2} + 4V_{g}^{2}}](/csm/wiki/images/math/b/3/1/b31e48307d48a44f52909ebe9a20a3a5.png)
Where εo is the free electron energy, b is a reciprocal lattice vector, and Vg is the Fourier component of the potential. It can be seen that at the zone boundaries there is a forbidden gap equal to twice the magnitude of the Fourier amplitude.
Consider a simple case where there is consider a parabolic band dispersion centered at 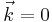 . If, at zero temperature the valence band is completely full and the conduction is partially full, the material is a metal.
. If, at zero temperature the valence band is completely full and the conduction is partially full, the material is a metal.
Boltzmann Transport
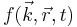 can be interpreted as the concentration of electrons in a state k, near a point r, at time t (Askerov chap 3).
can be interpreted as the concentration of electrons in a state k, near a point r, at time t (Askerov chap 3).
Electrical Current
The electrical current density is given by
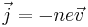
The number density is given by
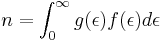
The current density may now be rewritten by plugging in the above equation for number density. When doing so, it must be remembered that the velocity is also a function of energy, and so it must be written inside of the integral.
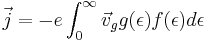
When considering a system at equilibrium, the current density is zero and the distribution function is the localized equilibrium distribution function, f0. Since the equilibrium current density equals zero, it may be subtracted from the current density with no consequence. The result is
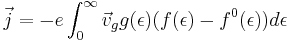
Using the Boltzmann transport equation to solve for (f(ε) − f0(ε)), the current density can be rewritten as
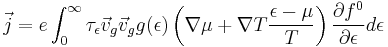
Heat Energy Flux Density (Thermal Current)
The thermal current is given by
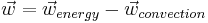
The energy current is caused by the flow of heat carrying electrons along a temperature gradient.
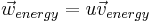
The energy density is given by
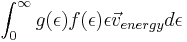
The convection current is the current caused by an external electric field.
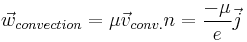
Using the above equations to solve for thermal current yields
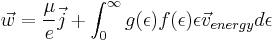
Similar to the process used in the derivation of the electrical current, we consider the steady state system. At steady state  are 0, so the convection current on its own must equal zero. At equilibrium the distribution function is written as the equilibrium distribution function f0. Since this term equals zero, it may be subtracted from the thermal current with no consequence.
are 0, so the convection current on its own must equal zero. At equilibrium the distribution function is written as the equilibrium distribution function f0. Since this term equals zero, it may be subtracted from the thermal current with no consequence.
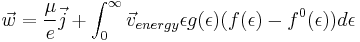
When substituting the Boltzman transport equation solved for f(ε) − f0(ε) the thermal current is written as
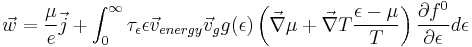
Boltzmann Equation
(Askerov chap 3)First lets consider what processes can bring about a change in the distribution function. There can be diffusion from temperature or concentration gradients, acceleration caused by external fields, and scattering by phonons or impurities. With this knowledge alone we can construct an expression for how the non equilibrium distribution function evolves with time.
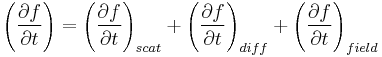
This is a primitive form of the Boltzmann equation. First consider the diffusion term. At a given time the concentration of electrons in a state k, near a point r will be 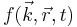 . After a time Δt the concentration is given by
. After a time Δt the concentration is given by 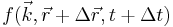 .
.
With the knowledge that
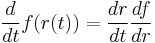
It can be shown that
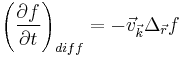
Next lets examine the effect of external fields. An external force F will cause the wave vector to vary in time such that
\frac{d \vec{k}}{dt} = \frac{\vec{F}}{\hbar}
Thus after a time Δt the distribution is 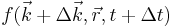 . Following the same logic as above it can be shown that
. Following the same logic as above it can be shown that
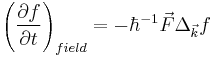
Assume the external force will be determined by the Lorentz force equation and we are limited to the stationary case such that 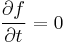 . With this we can rewrite the Boltzmann equation as
. With this we can rewrite the Boltzmann equation as
![\vec{v}(\vec{k}) \Delta_\vec{r} f - \frac{e}{\hbar} \left( E_o + \frac{1}{c} [\vec{v}(\vec{k}) \vec{H}]\right) \Delta_{\vec{k}} f = \left( \frac{\delta f}{\delta t} \right)_{scat}](/csm/wiki/images/math/a/e/e/aee42329ce0ee8bd0a0aa0378fd1436d.png)
The Relaxation Time approximation
The general Boltzmann equation is not conducive to analytical solutions and many times a relaxation time approximation is made. This introduces a mean time between scattering events, termed the relaxation time, τ. The relaxation time scales linearly with the Hall angle. This approximation is only appropriate when the change in energy associated with a scattering event is small compared to the initial and final energies (Harman 209). One interpretation of the relaxation time is to say that it characterizes the how quickly the system returns to equilibrium (Askerov).
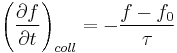
(Harman, 115)
Characterizing the Relaxation Time
Perhaps the most general way to express the relaxation time is as follows:
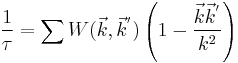
Where the sum is over k' and the quantity 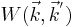 is the probability of transition from k to k' per unit time. The form of the transition probability is complex and depends on the particular scattering mechanism considered.
is the probability of transition from k to k' per unit time. The form of the transition probability is complex and depends on the particular scattering mechanism considered.
For a detailed look at how τ is determined, let us first consider acoustic phonon scattering.[2]
It is shown in Askerov that the relaxation time for an arbitrary spherically symmetric band can be expressed
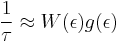
Scattering
In general, carriers moving throughout a lattice can be subjected to six different scattering mechanisms. The various scattering centers are: acoustic phonons, optical phonons, ionized and neutral impurities, electron-hole interactions, electron-electron interactions, and scattering due to elastoresistance and piezoresistance effects.
Transport Integrals
Defining the following integral will make expressions easier to understand.
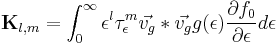
Two approximations can be made to transform this expression into the familiar Fermi integral.
Transport Coefficients
Electrical Conductivity
Electrical conductivity is a quantity that relates a materials current response to an electric field. The constitutive relation describing this phenomena is known as ohm's law.
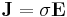
Taking 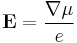 and letting
and letting 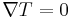 the current expression above we can write the conductivity as
the current expression above we can write the conductivity as
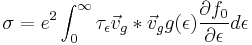
or
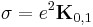
Thermal Conductivity
Thermal conductivity describes a materials ability to conduct heat. There are multiple contributions to thermal conductivity.
KT = κe + κph + κbi + κpt
Phonon Contribution
Phonons are vibrational modes that occur in a lattice.
Electron contribution The electron contribution is often approximated via the Wiedemann-Franz relation
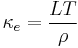
Where T is temperature, ρ is resistivity, and L is Lorenz number, which is in general a function of reduced chemical potential.
Photon contribution Negligible
Bipolar contribution Refers to excitons moving through the lattice and recombining, releasing energy.
In the context of thermoelectrics, the goal is to reduce thermal conductivity.
Seebeck
The seebeck effect describes the creation of a voltage across a material in response to a temperature gradient. From mahan book chapter 11. Consider a bar of material of length L. Assume a temperature gradient such that
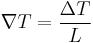
The material is insulated so, 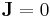 . Then there will be electric field between the ends given by
. Then there will be electric field between the ends given by
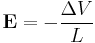
The ratio of these quantities is a property intrinsic to a material and described via the Seebeck coefficient.
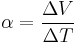
Letting 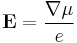 This can also be written as:
This can also be written as:
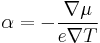
From this definition for the Seebeck coefficient, we are now in a position to derive an expression for this quantity via more rigorous expressions for current. Consider the expression for electrical current shown in a previous section. Letting 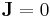

Now distribute through the quantity in parentheses
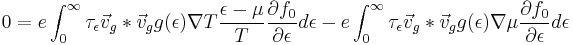
This expression in terms of the K integrals previously defined is
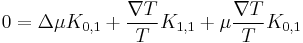
Now solve for 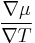 and the Seebeck coefficient can be written as
and the Seebeck coefficient can be written as
Physically the Seebeck effect can be explained by the propagation of electrons from the hot side of the material to the cold side.
Peltier
This process is analogous to the seebeck effect. Some materials will absorb heat when a current is passed through it. The peltier coefficient can be defined as the ratio of the heat carried by the charges to the current across the material.
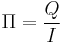
The peltier coefficient can also be related to the seebeck coefficient:
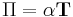
Hall
Examination of the Hall effect provides valuable information regarding the conduction properties of semiconductors.
Quote from Lindberg paper: "The Hall effect provides a direct measurement of the carrier type and concentration and, in conjunction with the resistivity, yields the mobility."
In addition, the Hall effect can give an accurate measurement of the impurity level. Consider a substance carrying a current in the x-direction with a magnetic field applied in the z-direction. An E-field will occur in the y-direction and is called the Hall field. The Hall field will be proportional to the product of the current density and the magnitude of the applied magnetic field. The constant of proportionality is the Hall Coefficient.
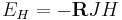
The Hall effect allows for the determination of carrier concentration and mobility. The Hall effect can be explained from a semi-classical standpoint.
Nernst
Consider a sample with a thermal current in the x-direction and a magnetic field in the z-direction. An electric field will be induced in the y-direction.
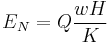
Where Q is the Nernst coefficient, w is the thermal current, H is the magnetic field perpendicular to current flow, and K is the thermal conductivity of the sample.
Ettingshausen
Consider a sample with a current flow in the x-direction and an applied electric field in the z-direction. If this occurs a temperature gradient will appear in y-direction.
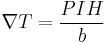
Where P is the Ettingshausen coefficient, I is the current, H is the magnetic field perpendicular to current flow, and b is the thickness of the sample.
Righi-Leduc
This effect produces a temperature gradient in the y-direction when a thermal current is applied in the x-direction, and a magnetic field is applied in the z-direction.
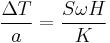
Where a is the width of the sample, ω is the thermal current and K is the thermal conductivity of the sample.
Thermoelectrics
Figure of Merit
It is now worth noting the thermoelectric figure of merit zT.
Maximizing this quantity can be difficult considering the somewhat contradictory requirements of high seebeck, high conductivity, and low thermal conductivity. Many efforts have focused on the reduction of the lattice component of thermal conductivity.
This figure of merit has led researchers to pursue materials that have high electrical conductivities such as those associated with rigid crystals, and low thermal conductivity such as amorphous materials. This has led to the term phonon glass electron crystal (PGEC).
Beta Parameter
Chasmar and Stratton introduced an alternative figure of merit that can be derived from zT. The derivation makes use of the following expressions and is illustrated in document below. Note that in the section below θ is used to represent the seebeck coefficient.
σ = σ0ε(η) =
θ = (k / e)(η − δ)
κn = Δ(k / e)2Tσ
Also,
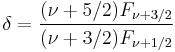
![\Delta = \frac{(\nu+7/2)F_{\nu+5/2}}{(\nu+3/2)F_{\nu+1/2}} - \left[\frac{(\nu+5/2)F_{\nu+3/2}}{(\nu+3/2)F_{\nu+1/2}}\right]^2](/csm/wiki/images/math/8/0/6/8062780968b381a92294d93dadb66ce0.png)
where,
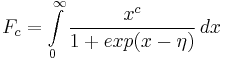
For a detailed manipulation of going from zT to beta, click this link [3]
This figure of merit, termed the beta parameter or material factor, is dimensionless quantity that can be written as:
β = (k / e)2Tσ0 / κl
References
Textbooks
- ↑ Schroeder, Daniel V. Thermal Physics. 2000
- ↑ Fistul V. "Heavily Doped Semiconductors". 1969
- ↑ Mahan, Gerald.Condensed Matter in a Nutshell. 2010
- Schroeder, Daniel V. Thermal Physics. 2000
- Kittel, Charles. Solid State Physics. 2005
- Griffiths. David. Introduction to Quantum Mechanics. 2005
- Mahan, Gerald.Condensed Matter in a Nutshell. 2010
- Lindsay, S.M. Introduction to Nanoscience. 2009
- Nolas, G.S. Thermoelectrics: Basic Principles and New Materials Developments. 1962
- Ashcroft and Mermin. Solid State Physics. 1976
- Harman & Honig. Thermoelectric and Thermomagnetic Effects and Applications. 1967
- Askerov B.M. "Electron Transport Phenomena in Semiconductors". 1994
- Fistul V. "Heavily Doped Semiconductors". 1969
Papers
- Snyder J.G. & Toberer E.S., Complex Thermoelectric Materials. Nature, 7 105-114 (2008).
- Mahan G.D., The Best Thermoelectric. 93 7436-7439 (1996).
- Zevalkink A & Toberer E.S., Ca3AlSb3: An inexpensive, non-toxic thermoelectric material for waste heat recovery. Energy Environ. Sci., 4, 510-518 (2011).
- Lindberg O, Hall Effect. (1952).
- Chasmar R.P. & Stratton R., The Thermoelectric Figure of Merit and its Relation to Thermoelectric Generators. Research Department, Metropolitan-Vickers Electrical Co. Ltd. (1959).
- Martinez A. Unpublished report (2011).
- Young D.L., Coutts T.F., et. al., Direct measurement of density-of-states effective mass and scatter parameter in transparent conducting oxides using second-order transport phenomena. Am. Vac. Soc. (200)
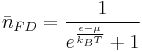
![\alpha=\frac{1}{eT}\left[\mu-\frac{K_{1,1}}{K_{0,1}}\right]](/csm/wiki/images/math/b/9/0/b90b2d440041f8cf309cfc970592d61a.png)