PHGN-471 Fall-2011
| Line 24: | Line 24: | ||
===Distribution Functions=== | ===Distribution Functions=== | ||
| + | Distribution functions are functions that have little importance on their own, but when integrated form a meaningful value, like a probability. Three distribution functions will be examined; the Maxwell distribution, the Fermi-Dirac distribution, and the Bose-Einstein distribution. | ||
| + | ====Maxwell Distribution==== | ||
| + | Begin by considering an ideal gas. We will want to consider the motions of an individual molecule within the gas. More specifically, we will ask the question "What is the probability of a particular molecule moving at a given speed?". There are infinitely many speeds that the molecule may travel at, so the probability of the speed being a particular one is nearly zero. But relative to each other, some speeds are more probable than others so the relative probability of each speed must be considered. A plot of the relative probability for each speed ''v'' is shown below. This graph is normalized (the area underneath the curve is 1) so the area between two speeds is the probability that a molecule's speed is within the specified range. | ||
| + | |||
| + | INSERT GRAPH OF D(V) | ||
| + | |||
| + | The graph shows D(''v''), but what is D(''v'')? The equation below describes the two factors in the equation | ||
| + | |||
| + | <math>D(\textit{v})\propto(\text{Probability of molecule having }\vec{v})\times(\text{the number of vectors }\vec{v}\text{ corresponding to }\textit{v})</math> | ||
| + | |||
| + | The probability of a molecule having <math>\vec{v}</math> is given by the Boltzmann Factor, <math>e^{\frac{-E(s)}{k_BT}}</math>. In the ideal gas, the total energy is due purely to the kinetic so <math>E(s)=\frac{1}{2}m\textit{v}^2</math> The second factor in the equation can be found by considering 3 dimensional velocity space. In this space, the number of vectors <math>\vec{v}</math> corresponding to ''v'' is the surface of a sphere of radius ''v''. | ||
| + | |||
| + | <math>\text{Surface Area} = 4\pi v^2</math> | ||
| + | |||
| + | D(''v'') is normalized, so the surface area, the Boltzmann factor, and a normalizing constant must be integrated from 0 to infinity and set equal to 1. Solving this for the normalizing constant completes Maxwell's distribution. | ||
| + | |||
| + | <math>D(v)=(\frac{m}{2 \pi k_B T})^{\frac{3}{2}} 4 \pi m v^2 e^{\frac{-mv^2}{2k_BT}}</math> | ||
===Independent, Free Electron Gas=== | ===Independent, Free Electron Gas=== | ||
Revision as of 04:00, 27 September 2011
| Main Page | > | Physics Course Wikis |
Contents
|
Course Information
Instructor: Eric Toberer
Research Assistant: Aaron Martinez
Students: Kyle Conrad and Michael Dixon
Project Title: Predicting the electronic behavior of thermoelectric materials via the Boltzmann transport equation
Objective
Understanding electronic transport in semiconductors materials is critical for the development of advanced thermoelectric materials of energy harvesting. To date, modeling thermoelectric materials typically involves applying solutions to the Boltzmann transport equation within the limit of a single parabolic band. This senior design project will consider the effect of non parabolic bands, multiple bands, and inter-band scattering on the predicted properties of thermoelectric materials.
The goal of this project is to use the advanced transport expressions to determine an optimal thermoelectric band structure and develop guidelines for the selection of thermoelectric materials.
Transport Theory
Density of States
Distribution Functions
Distribution functions are functions that have little importance on their own, but when integrated form a meaningful value, like a probability. Three distribution functions will be examined; the Maxwell distribution, the Fermi-Dirac distribution, and the Bose-Einstein distribution.
Maxwell Distribution
Begin by considering an ideal gas. We will want to consider the motions of an individual molecule within the gas. More specifically, we will ask the question "What is the probability of a particular molecule moving at a given speed?". There are infinitely many speeds that the molecule may travel at, so the probability of the speed being a particular one is nearly zero. But relative to each other, some speeds are more probable than others so the relative probability of each speed must be considered. A plot of the relative probability for each speed v is shown below. This graph is normalized (the area underneath the curve is 1) so the area between two speeds is the probability that a molecule's speed is within the specified range.
INSERT GRAPH OF D(V)
The graph shows D(v), but what is D(v)? The equation below describes the two factors in the equation
The probability of a molecule having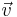 
is given by the Boltzmann Factor, 
. In the ideal gas, the total energy is due purely to the kinetic so 
The second factor in the equation can be found by considering 3 dimensional velocity space. In this space, the number of vectors 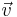corresponding to v is the surface of a sphere of radius v.
Surface Area = 4πv2
D(v) is normalized, so the surface area, the Boltzmann factor, and a normalizing constant must be integrated from 0 to infinity and set equal to 1. Solving this for the normalizing constant completes Maxwell's distribution.
Independent, Free Electron Gas
Boltzmann Transport
Electrical Current
