Modern 2:More on Square Wells and Review for Monday's Exam
(Difference between revisions)
| Line 9: | Line 9: | ||
In addition to this summary, you should understand | In addition to this summary, you should understand | ||
| − | + | * the ininite square well sufficiently to be able to derive the energy eigenstates, the energy levels and normalization. | |
| − | + | * the eigenstates are orthogonal and complete. This lets us represent any wavefunction as a superposition of eigenstates. | |
| − | + | * if the wavefunction IS an eigenfunction of some observable <math>\hat{A}</math> with eigenvalue <math>a</math>, the the measurement of <math>A</math> is equal to <math>a</math> with probability 1. | |
| − | <math>a</math>, the the measurement of <math>A</math> is equal to <math>a</math> with probability 1. | + | |
Revision as of 16:07, 10 March 2006
There is a review of important topics at the end of chapter 3, pages 58-59. I will go over this
in class today. But briefly, it includes the time dependent and time independent Schrodinger equations.
Momentum space representation. The Heisenberg uncertainty relation (for x, p_x and E, t). The idea that
to each physical quantity A there is an associated observable
given as a self-adjoint operator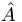 
. And that
the expected value of a measurement associated with this quantity is given by ![\langle \psi
|\hat{A}|\psi \rangle = \int \psi^*(\mathbf{r},t) \left[ \hat{A} \psi(\mathbf{r},t) \right] d^3 r](/csm/wiki/images/math/c/1/2/c1247c7e65273b11e9d6e16a338c18bd.png)
.
In addition to this summary, you should understand
- the ininite square well sufficiently to be able to derive the energy eigenstates, the energy levels and normalization.
- the eigenstates are orthogonal and complete. This lets us represent any wavefunction as a superposition of eigenstates.
- if the wavefunction IS an eigenfunction of some observable 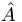with eigenvalue a, the the measurement of A is equal to a with probability 1.
