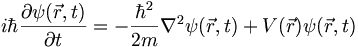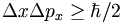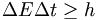Modern 2:Measurements and Eigenstates
| Line 14: | Line 14: | ||
Let us define an operator for the total energy (kinetic plus potential). This is called the Hamiltonian | Let us define an operator for the total energy (kinetic plus potential). This is called the Hamiltonian | ||
| − | <math> \hat{H} = \frac{ | + | <math> \hat{H} = \frac{{\vec{p}}^2}{2m} + \hat{V} = </math> |
| + | |||
| + | <math> - \frac{\hbar^2}{2 m} \nabla^2 \psi(\vec{r}, t) + V(\vec{r}) </math> | ||
===measurements uncertainty=== | ===measurements uncertainty=== | ||
Revision as of 15:41, 27 February 2006
states with precisely known energy
Here is the Schrodinger equation for a nonrelativistic particle in an external, time-independent potential
We'll be working on this equation for the rest of the semester! In the homework you will prove that the position-space represnetation of the momentum operator is given by
(3.9) 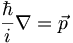
I'm going to rewrite this using a hat over the momentum to indicate the fact that it is really an operator:

Let us define an operator for the total energy (kinetic plus potential). This is called the Hamiltonian


measurements uncertainty
We have seen that in general if N copies of a system are prepared in identical states, then the result of any measurement will have a statistical spread of values. Further, there is a fundamental connection between the uncertainty of an observable and that of its Fourier transform pair. E.g.,
It would be nice if we could expect something like
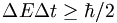
to be true, but it's not obvious.
John Baez on the time/energy uncertainty relation
One of the reasons it's not obvious is that there while there is an energy operator in QM (the Hamiltonian), there is no time operator in QM!
It turns out that from the Fourier transform ideas we've talked about you can show that:
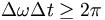
which then gives (using Einstein's relation)
NB: that is not