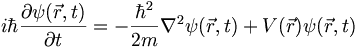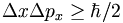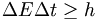Modern 2:Measurements and Eigenstates

Course Wikis

>

Physics Course Wikis

>

Modern 2

states with precisely known energy

Here is the Schrodinger equation for a nonrelativistic particle in an external, time-independent potential

$i \hbar \frac{\partial \psi(\vec{r}, t)}{\partial t} = - \frac{\hbar^2}{2 m} \nabla^2 \psi(\vec{r}, t) + V(\vec{r}) \psi(\vec{r}, t)$

We'll be working on this equation for the rest of the semester! In the homework you will prove that the position-space represnetation of the momentum operator is given by

(3.9) 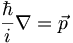$\frac{\hbar}{i} \nabla = \vec{p}$

I'm going to rewrite this using a hat over the momentum to indicate the fact that it is really an operator:

$\frac{\hbar}{i} \nabla = \hat{\mathbf{p}}$

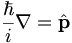
Let us define an operator for the total energy (kinetic plus potential). This is called the Hamiltonian

$\hat{H} = \frac{{\vec{p}}^2}{2m} + \hat{V}$

$= - \frac{\hbar^2}{2 m} \nabla^2 + V(\vec{r})$

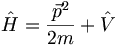
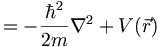
Using this we can rewrite the Schrodinger equation as

(3.16)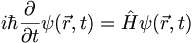 $i \hbar \frac{\partial}{\partial t} \psi(\vec{r}, t) = \hat{H} \psi(\vec{r}, t)$

Normally we expect that the result of repeated measurments of systems prepared identically will yield a spread of results. But there are clearly some measurement which lead to very precise and repeatable measurements, such as spectral lines, narrow-band laser frequencies, etc. So let us consider the case in which the time dependence of the wave function is a constant frequency sinusoid. I.e., suppose that

$\psi(\vec{r},t) = \psi(\vec{r}) e^{-i \omega t} = \psi(\vec{r}) e^{-i E t/ \hbar}$

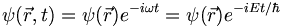
A constant frequency means a constant energy. So if we plug this kind of wavefunction into 3.16 the Schrodinger equation becomes

 (3.17)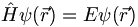 $\hat{H} \psi(\vec{r}) = E \psi(\vec{r})$

This is an example of an eigenvalue/eigenfunction problem. 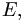$E ,\$ is an eigenvalue of the operator 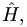$\hat{H} ,\$ associated with the eigenvector $\psi(\vec{r}) ,\$.

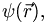examples of precisely determined measurements

spectral lines

optical spectroscopy

flux plot with nice java applet

nice NMR page

Observables

Study Principle 3.1 in the book carefully. It says that for any physical quantity 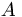$A \$ (e.g., position, angular momentum, energy, etc) there is an operator 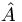$\hat{A}$ which we call the observable associated with 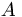$A \$, and that this operator is a linear Hermitian (self-adjoint) operator. We will denote by the lower case 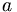$a \$ the result of a measurement of 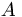$A \$. Then the expected value of such a measurement at any time 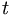$t \$ is given by

(3.5) $\langle a \rangle _ t = \int \psi^*(\vec{r},t) \left[ \hat{A} \psi(\vec{r},t) \right] d^3 r$

To understand this equation suppose that 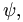$\psi ,\$ were an ordinary real vector and 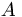$A \$ a matrix. Then we would write the RHS as

$\left( \psi, A \psi \right) \$

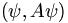
For a symmetric matrix this is equal to

$\left(A \psi, \psi \right) \$

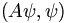
Proof: 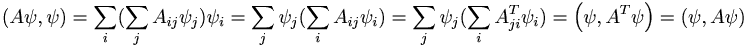$\left(A \psi, \psi \right) = \sum _ i ( \sum _ j A_{ij} \psi_j ) \psi_i = \sum _ j \psi_j (\sum_i A_{ij} \psi_i) = \sum _ j \psi_j (\sum_i A^T_{ji} \psi_i) = \left( \psi, A^T \psi \right) = \left( \psi, A \psi \right) \$

But this is for real vectors. For complex vectors, as we discussed in the last class, we need a complex conjugate in the inner product in order that the inner product of a vector with itself be real. All of these considerations led Dirac to invent a new notation for function inner products such as (3.5). In Dirac's bra-ket notation (3.5) becomes:

$\langle \psi | \hat{A} | \psi \rangle \$

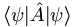
which for self-adjoint operators is equivalent to

$\langle \hat{A} \psi |\psi \rangle \$

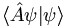
In this notation, the ket vector 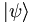$|\psi\rangle$ is different than the bra vector 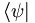$\langle \psi |$. In fact, we have

$\langle \psi | = |\psi\rangle ^{T*} = |\psi\rangle ^ \dagger$

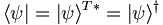
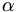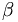Suppose $\alpha \$ and $\beta \$ represent two states of the system. Then the inner product of these two states is 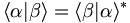$\langle \alpha | \beta \rangle = \langle \beta | \alpha \rangle^* \$. In coordinate space representation we would write this inner product as an integral (in one-dimension) as

$\int \psi ^* _\alpha (x) \psi_\beta (x) dx$.

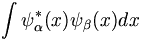Here is a minor, slightly picky bit of notation. We know that operators map vectors into vectors. Hence they map, say, ket-vectors into ket-vectors. So we denote by 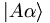$|A \alpha\rangle$ the ket which is obtained by operating on 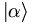$|\alpha\rangle$ by the operator $\hat A$:

$\hat{A} | \alpha \rangle = | A \alpha \rangle$

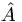operators have different algebraic properties than numbers or functions

Consider an operator equation

$\frac{\partial}{\partial x} \frac{\partial}{\partial y} - \frac{\partial}{\partial y} \frac{\partial}{\partial x}$

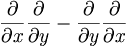
if these were numbers then this would clearly be zero. But for operators, this is shorthand for

$\left[ \frac{\partial}{\partial x} \frac{\partial}{\partial y} - \frac{\partial}{\partial y} \frac{\partial}{\partial x} \right] f(x,y)$

where f is some well-behaved function. In Quantum Mechanics a combination such as 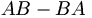$AB - BA \$ is called a commutator. We know from ordinary calculus that the commutator of partial derivatives is zero.

$[\frac{ \partial}{\partial x} , \frac{\partial}{\partial y}] = 0$

But what about

$[\frac{ \partial}{\partial x}, x]$ ?

HW not to be turned in: show that

$[\hat{x}, \hat{p}_x] = i \hbar \hat{I}$

where

$\hat{p}_x = -i \hbar \frac{\partial}{\partial x}$

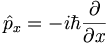
orthogonality of the eigenfunctions of self-adjoint operators

HW not to be turned in: prove the following. If ψ₁ and ψ₂ are two eigenfunctions of a self-adjoint operator with different eigenvalues, then ψ₁ and ψ₂ are orthogonal. I.e., 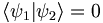$\langle \psi_1 | \psi_2 \rangle = 0$. An important example of this is the following:

Take 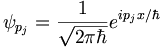$\psi_{p_j} = \frac{1}{\sqrt{2 \pi \hbar}} e^{ip_j x/\hbar}$ to be the normalized momentum eigenfunction for a free particle with momentum p_j then

$\int \psi ^* _{p_i}(x) \psi _{p_j}(x) dx = \langle p_i | p_j \rangle = \delta(p_i - p_j)$

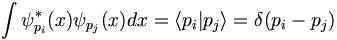
digression on the time/energy uncertainty relation

We have seen that in general if N copies of a system are prepared in identical states, then the result of any measurement will have a statistical spread of values. Further, there is a fundamental connection between the uncertainty of an observable and that of its Fourier transform pair. E.g.,

$\Delta x \Delta p_x \geq \hbar /2$

It would be nice if we could expect something like

$\Delta E \Delta t \geq \hbar/2$

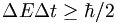
to be true, but it's not obvious.

John Baez on the time/energy uncertainty relation

One of the reasons it's not obvious is that there while there is an energy operator in QM (the Hamiltonian), there is no time operator in QM!

It turns out that from the Fourier transform ideas we've talked about you can show that:

$\Delta \omega \Delta t \geq 2 \pi$

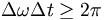
which then gives (using Einstein's relation)

$\Delta E \Delta t \geq h$