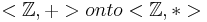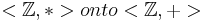Homework 2

1. Suppose that * is an associative and commutative binary operation on a set S. Show that 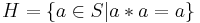$H = \{a \in S | a*a = a\}$ is closed under *.
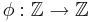2. The map $\phi:\mathbb{Z} \rightarrow \mathbb{Z}$ defined by φ(n) = n + 1 for integer n, is one to one and onto. Give the definition of a binary operation * on the integers such that φ is an isomorphism mapping
   1. $<\mathbb{Z},+> onto <\mathbb{Z}, *>$
   2. $<\mathbb{Z},*> onto <\mathbb{Z},+>$
3. Let H be the subset of 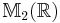$\mathbb{M}_2(\mathbb{R})$ consisting of all matrices of the form 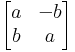$\begin{bmatrix} a & -b\\ b&a \end{bmatrix}$ for a,b in the reals. Show that 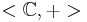$<\mathbb{C},+>$ is isomorphic to < H, + > .
4. Let S = {e,a,b,c} with e the identity element for the corresponding group operation. Find all possible group structures for < S, * > by constructing the corresponding Cayley table(s). Are any of the tables you found isomorphic? How many unique structures did you find?
5. For * defined on 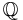$\mathbb{Q}$ by a * b = ab, determine if 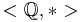$<\mathbb{Q},*>$ is a group. If not, specifically which axioms fail?
6. Determine if < S, * > is a group where S is the set of all 2 x 2 matrices with diagonal entries either 1 or -1 and * is defined to be matrix multiplication.
7. Let G be the following set of matrices
   $\left\{ \begin{bmatrix} 1 & 0\\0 & 1 \end{bmatrix}, \begin{bmatrix} x&0\\ 0 & x^2\end{bmatrix}, \begin{bmatrix} x^2 & 0\\0 & x \end{bmatrix}, \begin{bmatrix} 0 & 1\\1 & 0 \end{bmatrix}, \begin{bmatrix} 0 & x^2\\x & 0 \end{bmatrix}, \begin{bmatrix} 0 & x\\x^2 & 0 \end{bmatrix} \right\}$
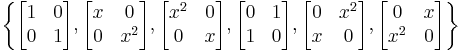
   where x³ = 1 but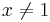 $x \ne 1$. Show that G under matrix multiplication is a group. Also, show that $G \simeq D_3$ (the dihedral group discussed in class).