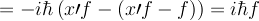Exam 2

test 2

• problem 1

$\frac{- \hbar ^2}{2m} \frac{d^2}{dx^2} \psi(x) = E \psi(x)$

$\psi(-a/2) = \psi(a/2) = 0 \$

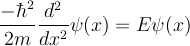
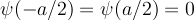
Inside the well we should expect plane wave solutions:

$\psi(x) = A e^{i k x} + B e^{-ikx} \$

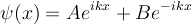
Where 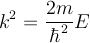$k^2 = \frac{2m}{\hbar ^2} E \$

Applying the BC this gives:

$A e^{-ika/2} + B e^{ika/2} = 0\$

$A e^{ika/2} + B e^{-ika/2} = 0\$

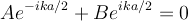
At this point you have two equatins and two unknowns. I don't care how you solve them. Here is one way. Add the two equations to get:

$2A \cos(ka/2) + 2B \cos(ka/2) = 0 \$

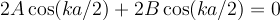
now subtract to get:

$2iA \sin(ka/2) - 2iB \sin(ka/2) = 0\$

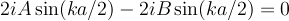
These are nice since we can factor out the common sine and cosine terms:

$(A+B) \cos(ka/2) = 0 \$

$(A-B) \sin(ka/2) = 0 \$

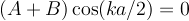
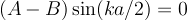
There are only two ways we can satisfy both equations simultaneously. If A=B then the second equatino is taken care of, but then A+B cannot = 0, so we have to insist that 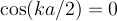$\cos(ka/2) = 0 \$. This requires

$ka/2 = (n-1/2) \pi \$

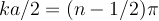
On the other hand, if we choose A = -B, then the first equation is automatically satisfied and then we must insist that 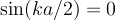$\sin(ka/2) = 0 \$. This requires

$ka/2 = n \pi \$

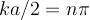
So we have two families of solutions:

$\psi(x) = A \left(e^{i k x} + e^{-ikx} \right) = A \cos \left( \frac{2 \pi (n-1/2)}{a} x \right) \$

$\psi(x) = B \left(e^{i k x} - e^{-ikx} \right) = B \sin \left(\frac{2 \pi n}{a} x \right) \$

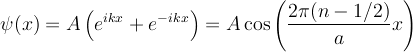
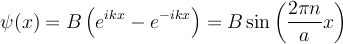
The cosine states are even (have even parity), the sine states are odd (have odd parity)

Now since 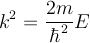$k^2 = \frac{2m}{\hbar ^2} E \$ we have

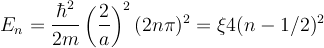$E_n = \frac{\hbar^2}{2m} \left( \frac{2}{a} \right) ^2 (2 n \pi)^2 = \xi 4(n-1/2)^2 \$ for the odd parity states and

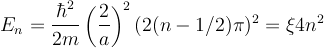$E_n = \frac{\hbar^2}{2m} \left(\frac{2}{a} \right)^2 (2 (n- 1/2) \pi)^2 = \xi 4 n^2 \$ for the even parity states.

In numerical order these are:

$\xi \times \{ 1, 4, 9, 16, ... \}$

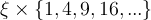
• problem 5

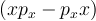$[x,p_x] \$ is an operator equation. By definition it is: $(x p_x - p_x x) \$. In order to work this out it is helpful to apply the operator to a test function.

$[x,p_x] f(x) = (x p_x - p_x x)f(x) = (x (-i \hbar d/dx)) f(x) - ((-i \hbar d/dx) x) f(x)$ $= -i \hbar \left( x \prime{f} - (x \prime{f} - f) \right) = i \hbar f$