Coherent states versus number (harmonic oscillator) states

The most wave-like state of a cavity is called a coherent state

• The harmonic oscillator states we wrote $|n \rangle$.

• We saw that hese states also arise when quantizing fields such as the electric field in a cavity and the displacement field in an elastic solid. In that case $n \$ refers to the number of quanta in the cavity or solid (we called these photons and phonons, respectively). In that context these are also called number states or Fock states.

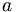• A quantum state of a cavity that is like a classical state as much as possible should have the property that when you make a measurement you don't change the state. Since nearly all measurements of light involve destroying photons (e.g., by creating current or heat), these measurements should have the general form some operators $\times a$ where $a \$ is the destruction (lowering) operator.

• This means that a quantum state that is "like a classical state" (whatever that means) should be an eigenvector of the destruction operator. Such states are called coherent states and were introduced by Roy Glauber, who was one of three people to get the Nobel Prize in Physics in 2005.

Roy Glauber @ Harvard

Here are two views of coherent states (both images from [1] Wikipedia):

You may recall that we showed that for the harmonic oscillator, the uncertainty in position and the uncertainty in momentum were exactly the same. The analagous result is true for coherent states. Namely the real and imaginary part of the electric field (or the x and y components) have the same uncertainy.

In the general case, in which the uncertainty is not evenly distributed between the two components of the electric field, the state is called a squeezed state.

the most unclassical states: number states

At the opposite extreme from coherent states are our old friends the harmonic oscillator (number) states. These are also called Fock states, after the Russian physicist Vladimir Fock.

Think about it, if you there are exactly n photons in a cavity, then the result of a measurement (at least a normal destructive measurement) must lead to a different number state after the measurement.

Further, if you know the number of photons in the cavity (and hence the energy) exactly, then the phase of the electric field must be completely unknown. This is analagous to the situation with the NH3 molecule where the energy eigenstates were delocalized about the two potential wells. You could initialize the system in a semi-classical state localized about the left or right well, but it would the oscillate back and forth between these two states.

the Wigner function

Consider, once again, the harmonic oscillator state 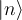$|n \rangle \$. Our cavity interpretation of this state is that it corresponds to having exactly n photons. Assuming we know the frequency of the light, this means we know the energy of the cavity. Hence the time (or phase) of the E field must be unknown. So this is the most unclassical of states.

A comment mathematical technique for studying these issues is the Wigner transformation (or Wigner function) of the wavefunction:

$W(x,p) = \frac{1}{2 \pi} \int _ {-\infty} ^ {+\infty} d\xi \exp(-i/\hbar \ p \xi) \psi^*(x - 1/2 \ \xi) \psi(x + 1/2 \ \xi)$

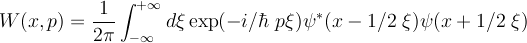
The Wigner function has the following important properties:

• $\int _ {-\infty} ^ {+\infty} dp W(x,p) \equiv W(x) = |\psi(x)|^2$
• $\int _ {-\infty} ^ {+\infty} dx W(x,p) \equiv W(p) = |\phi(p)|^2$
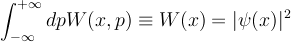
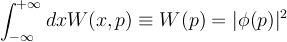
• Nevertheless, the Wigner function can be negative!

Here is a short piece of Mathematica for computing the Wigner function for Fock states:

\[Psi][n_, x_] := 1/Sqrt[Sqrt[Pi]2^n n!] Exp[-x^2/2]HermiteH[n, x]

f[n_, x_, y_] := Conjugate[\[Psi][n, x - 1/2 y]] \[Psi][n, x + 1/2 y]

k = 0

W[x_, p_] = NIntegrate[Exp[-I p y] f[k, x, y], {y, -10, 10}, MaxRecursion -> 10, Method -> Oscillatory]

Plot3D[Re[W[x, p]], {p, -5, 5}, {x, -5, 5}, PlotRange -> All, PlotPoints -> 50]

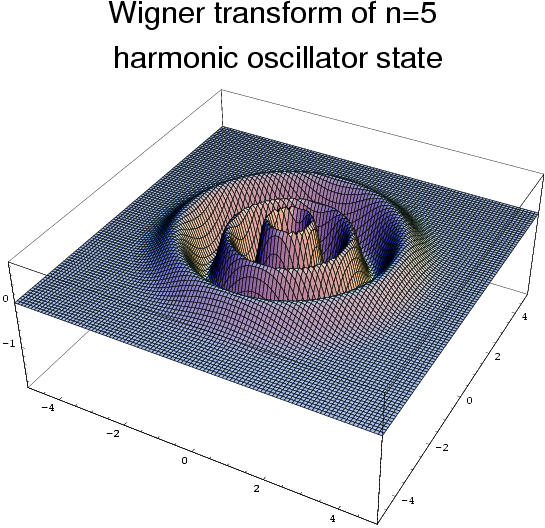
If you run this, be aware that when k > 0 you'll likely get a bazillion warnings about convergence. These integrals are hard to do numerically. Still, if you're patient (for each k value the calculation will take several minutes), you'll get nice results such as shown below.

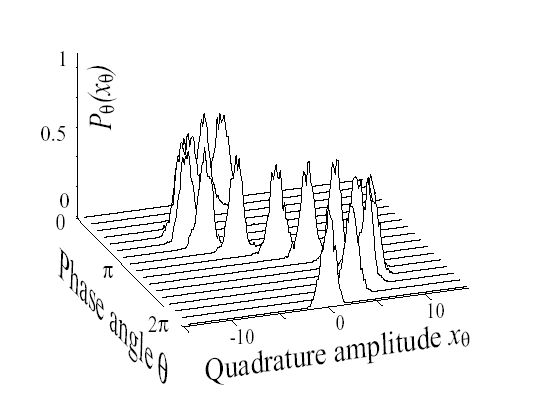
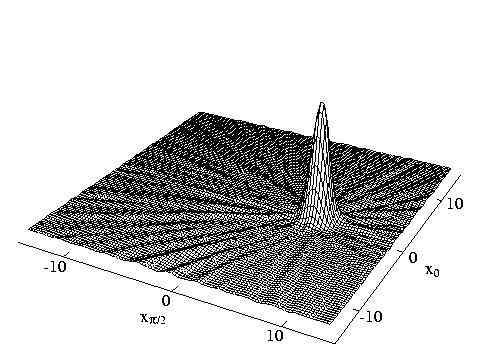
Here is an experimentally determined coherent state Wigner function due to Gerd Breitenbach.

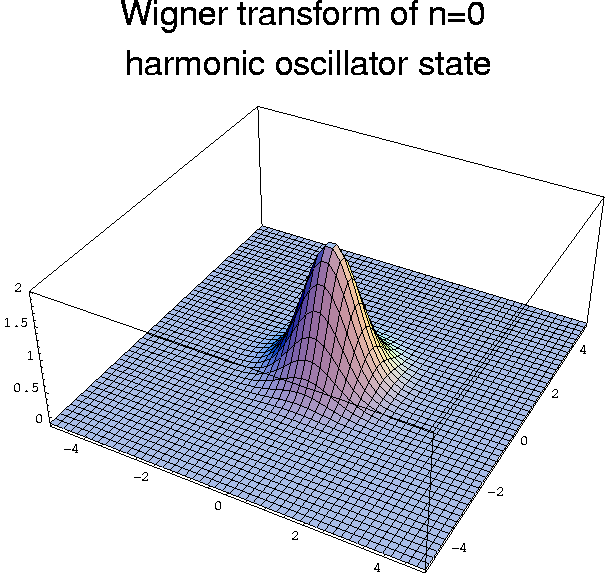
Experimentally youc an realize a coherent state by what amounts to pulling a mass on a spring down and letting it go. In this case we take the ground or vacuum state, whose Wigner function is

and suddenly displace the harmonic potential.

In general, the Wigner function for 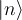$| n \rangle$ will have n+1 nodes corresponding to n = 0, 1, 2, ...

A gallery of Wigner functions

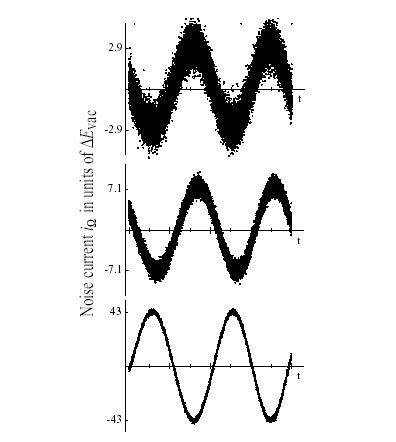
Some extremely beautiful measurements from David Wineland's group at NIST: [2].

And a further link to some of Wineland's work on quantum computing: [[3]]

Experiments like these are hard: [4] [5]