Bnibling/Acoustic Lab
Harmonics
Barrett Nibling
December 4th, 2007
Contents |
Abstract
This experiment dealt with the unique frequency patterns, known as harmonics, that sound produces in a resonator. Using white noise generated by a computer and transmitted through a speaker into our resonant cavity, a pipe, and at the other end was placed a microphone to record the outgoing frequencies. Using the geometry of the pipe and derived equations, theoretical values were calculated were calculated and compared to the measured values. The experimental data was within <insert %>% of the theoretical data.
List of Figures
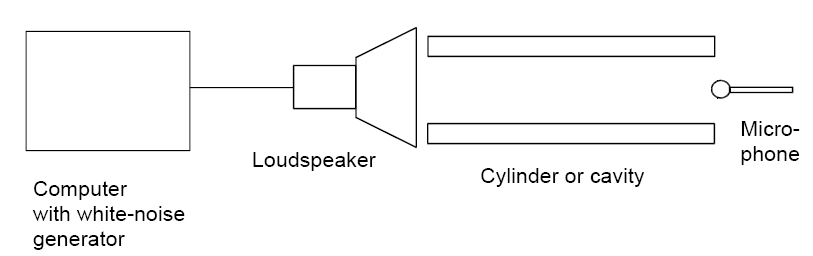
[1] Schematic of Harmonics Apparatus
Introduction
Sound produces unique frequency patterns when travelling through a resonant cavity, such as a tube, known as harmonics. These patterns depend on the frequencies sent into the body, the material, but more importantly the geometry of the structure. A computer was used to produce sound waves in the form of white noise through a speaker into one end of the cavity and by placing a microphone recording the frequency patterns on the other end, we could record the data on the computer for analysis. The computer software represents the data as a plot and the patterns on a graph shows the resonant peaks which occured in the cavity. These peaks can then be compared to expected peaks by using previously derived equations for the tubes we used. The derived peaks and the expected peaks were then compared and were found to agree within experimental error.
Theory
When a sound wave of a specific frequency enters a cavity, such as a musical instrument, the cavity will absorb the energy of the wave and produce a standing wave pattern that matches the resonant frequency. This only occurs when the specific frequency of the waves entering the system are close to the frequency of the acoustic resonance of the cavity. These resonant frequencies are known as harmonics. Each system of this type will have an infinite number of harmonics. The lowest frequency harmonic is called the fundamental frequency. Each harmonic following is a nth multiple of the fundamental frequency, known as the nth harmonics.
The constraint that determines the harmonic frequencies is the system itself. In the case of a pipe, which was used for our experiment, the resonance depends mainly on the length of the pipe. Since the pipe is open at both ends, the following previously derived equation can be used to approximate the harmonic frequency,
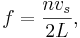
where n is a positive constant integer, vs is the speed of sound, and L is the length of the pipe. The speed of sound is given to be at 334 m/s[1]. This isn't the best equation that matches the model. The radius of the pipe effectively makes the pipe long, the bigger the radius, the more air the waves must travel through[2]. To account for this, the end correction factor of 0.6R, R being the radius of the pipe, must be implemented into the equation (1). Giving the following new equation,
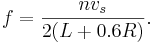
Procedure
Results
| Color | θdiff (degrees) | λ (nm) | Error (nm) | Published λ (nm) | |
|---|---|---|---|---|---|
| Purple | 15.6 | 448.0 |  2.0 2.0
|
447.148 | |
| Teal | 16.4 | 470.3 | 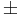 2.0 2.0
|
471.314 | |
| Green | 17.2 | 492.6 | 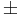 2.0 2.0
|
492.193 | |
| Green | 17.5 | 500.9 | 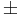 2.0 2.0
|
501.567 | |
| Yellow//Orange | 20.7 | 588.8 | 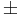 2.0 2.0
|
587.562 | |
| Red | 23.6 | 666.9 | 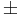 2.0 2.0
|
667.815 | |
| Dim Red | 25.1 | 706.7 |  1.9 1.9
|
??? |
Error Analysis
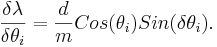
Then the total error is the sum of the two partial derivatives added in quadrature,
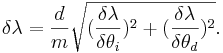
Conclusion
References
[1] speed of sound
[2] end correction http://www.phys.unsw.edu.au/jw/musFAQ.html#end