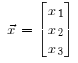Basics of Linear Algebra: Things you are supposed to know before Modern II

There are a few basic things you are supposed to know about Linear Algebra by spring of junior year. Most of this is covered in Math Physics, but that class has a lot of territory to cover, much of it seemingly unrelated to the rest, and as such many people have only very basic knowledge coming out of that class, and much of that is forgotten all too easily. This is a simple guide which illustrates many of the concepts at a basic level to clear up any confusion that may occur going into Modern Physics. The official Wikipedia pages dealling with the subject are: Vector Space Matrices Transpose Matrix Multiplication

Matrices and Vectors

There are three kinds of object you need to deal with. The first two are scalars and vectors, and the third is matrices. As you already know, scalars are just numbers, vectors are lists of numbers (like matrices but one dimension is of length one), and matrices are grids of numbers. These are all "tensors". There are more, higher ranked tensors, like 3-D grids of numbers, but those aren't so useful just now. Here are three generic objects:

x = x₁

Note that matrices are usually denoted by capital letters, and that operators (which are matrices) have hats. Also, rows are the first index, while columns are the second.

Transpose

The transpose of a matrix is simply the matrix with its rows turned into its columns, and vice versa. Another way to put it is that the matrix is reflected about its diagonal (the sequence of entries from top-left to bottom-right).

Also: 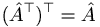$(\hat{A}^{\top})^{\top}=\hat{A}$

Adjoint

The adjoint of a matrix is simply the complex conjugate of the transpose. When one is using complex numbers almost all techniques that are typically used with the transpose of a matrix are instead used with the adjoint.

Matrix Multiplication

When two matrices are multiplied, each row (m) of the first is multiplied by each column (n) of the second, and the results are placed in the mth row and nth column of a new matrix. This multiplication is the vector dot product (the sum of the products of the nth row term with the nth column term). There are a few key points here. Firstly, since the columns of a matrix are generally not the same as its rows, matrix multiplication does not commute: 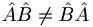$\hat{A} \hat{B}\neq \hat{B} \hat{A}$. However, it is true that 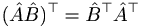$(\hat{A} \hat{B})^{\top}=\hat{B}^{\top} \hat{A}^{\top}$. A second point is that matrix multiplication only works like this if the number of columns in the first matrix equals the number of rows in the second. Thirdly, the product matrix has the same number of rows as the first matrix and the same number of columns as the second.

Finally, since vectors are just matrices with some number L rows and 1 column, all these rules apply to vectors. The dot product can therefore be described in terms of vector multiplication, as 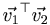$\vec{v_{1}}^{\top} \vec{v_{2}}$. This dot product is a 1x1 matrix, which is just a scalar to us. There are three main points to be made here, from the standpoint of Modern II.

• Firstly, in bra-ket notation the adjoint takes the place of the transpose here (which is necessary when working with complex numbers).
• Secondly, column (normal) vectors are exactly the same thing as kets, and row (adjoint) vectors are bras. Bra-ket notation essentially exists because you don't always know the exact numbers in a vector (or the numbers might change, in fact), and bra-ket notation lets you say something about the properties of operators and vectors without knowing anything specific about their actual contents.
• Thirdly, 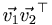$\vec{v_{1}} \vec{v_{2}}^{\top}$ is not the dot product, but actually a rather different object (sometimes called an "outer" product). Specifically, for vectors of length L, it is an LxL matrix. So although inner products are scalars and can move anywhere in an equation, vectors that are not moving as an inner product can not change order of multiplication. Neither can operators unless some symmetry condition lets them do so.