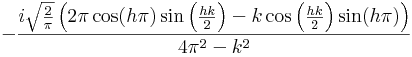Week of 11/5
| Line 38: | Line 38: | ||
{{mathematica|filename=Sincinterpolation.nb|title=Sinc function interpolation via the samping theorem}} | {{mathematica|filename=Sincinterpolation.nb|title=Sinc function interpolation via the samping theorem}} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | Mathematica can find the fourier transform of a box function of width h centered on zero times <math>sin(2 \pi x)</math>: | ||
| + | |||
| + | <math>-\frac{i \sqrt{\frac{2}{\pi }} \left(2 \pi \cos (h \pi ) \sin \left(\frac{h k}{2}\right)-k \cos \left(\frac{h k}{2}\right) \sin (h \pi )\right)}{4 \pi ^2-k^2} | ||
| + | </math> | ||
Revision as of 22:56, 5 November 2007
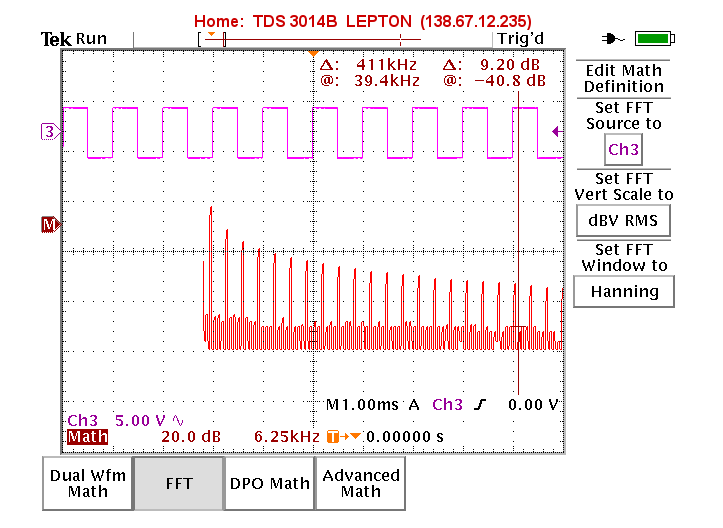
Here is the display of my oscilloscope when the input is a 1000 pulse per second output of a time-code generator. (The time-code generator is a device that locks to the 10 MHz output of an atomic clock and produces 1 Hz or 1 KHz pulse trains as well as human readable time synchronized to the atomic standard.)
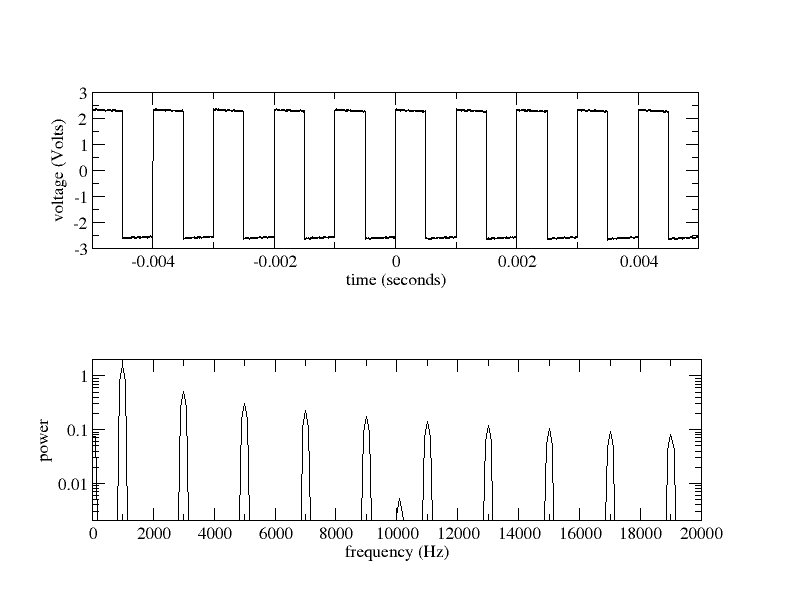
I imported the data and plotted it along with its periodogram.
Notice that only the odd harmonics are present.
Here is a mathematica notebook that simulates this.
 Download lots of fourier transform examples
|
Sampling theorem. See 10/31/07 lecture notes
We end up with
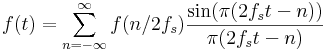
This amounts to taking samples of the data every 1 / 2fs and multiplying them by a sinc function and adding up the results.
| Download Sinc function interpolation via the samping theorem
|
Mathematica can find the fourier transform of a box function of width h centered on zero times sin(2πx):
