Week of 1/21/08
(Difference between revisions)
| Line 1: | Line 1: | ||
[http://mathworld.wolfram.com/HermitianInnerProduct.html Definition of complex (Hermitian) inner product] | [http://mathworld.wolfram.com/HermitianInnerProduct.html Definition of complex (Hermitian) inner product] | ||
| + | |||
| + | |||
| + | It's a matter of convention that the anti-linear term is the second one in the inner product: | ||
<math> \langle u+v,w \rangle \equiv \langle u,w \rangle + \langle v,w \rangle </math> | <math> \langle u+v,w \rangle \equiv \langle u,w \rangle + \langle v,w \rangle </math> | ||
| Line 16: | Line 19: | ||
<math>h(z,w) \equiv \sum z_i w^* _i</math> | <math>h(z,w) \equiv \sum z_i w^* _i</math> | ||
| + | |||
| + | NB if <math>z = x + I y</math>, then <math>z^* z = (x - I y)(x + I y) = x^2 + y^2 = z z^*</math> | ||
Revision as of 15:37, 21 January 2008
Definition of complex (Hermitian) inner product
It's a matter of convention that the anti-linear term is the second one in the inner product:
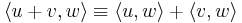
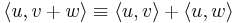
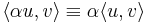
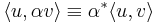
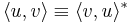
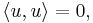 with equality only if
with equality only if 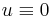
The basic example is the form
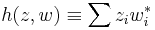
NB if z = x + Iy, then z * z = (x − Iy)(x + Iy) = x2 + y2 = zz *