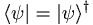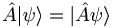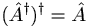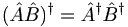Simple Bra-Ket Manipulations
(Difference between revisions)
Sean Santos (Talk | contribs) |
Sean Santos (Talk | contribs) |
||
| Line 1: | Line 1: | ||
| − | + | Here <math>\hat{O}</math> is an operator corresponding to some observable (like <math>\hat{H}</math> for energy), and its eigenvalues are <math>\lambda_{n}</math>. The corresponding eigenvectors are <math>\vert\phi_{n}\rangle</math>. <math>\vert\psi\rangle</math> is a generic state ket. <math>a_{n}</math> is the projection of <math>\vert\psi\rangle</math> onto <math>\vert\phi_{n}\rangle</math>. One of the keys to what follows is that the eigenvectors form an orthonormal basis. That just means that any vector can be built from a unique combination of <math>\vert\phi_{1}\rangle,\vert\phi_{2}\rangle,\vert\phi_{3}\rangle,\dots</math>, just like any vector in 3-D space can be built from a unique combination of x, y, and z, or any complex number can be built from 1 and i. | |
| − | + | ==Basics== | |
| + | ===Notation Definitions=== | ||
| + | *<math>\langle\psi\vert=\vert\psi\rangle^{\dagger}</math> | ||
| + | *<math>\hat{A}\vert\psi\rangle=\vert\hat{A}\psi\rangle</math> | ||
| + | ===From Linear Algebra=== | ||
| + | ====For All Vectors and Matrices==== | ||
| + | *<math>(\hat{A}^{\dagger})^{\dagger}=\hat{A}</math> | ||
| + | *<math>(\hat{A}\hat{B})^{\dagger}=\hat{A}^{\dagger} \hat{B}^{\dagger}</math> | ||
| + | ====For Hermitian Operators==== | ||
| + | *<math></math> | ||
Revision as of 19:02, 25 January 2007
Here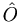 
is an operator corresponding to some observable (like 
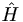for energy), and its eigenvalues are λn. The corresponding eigenvectors are 
. 
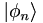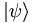is a generic state ket. an is the projection of 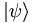onto 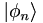. One of the keys to what follows is that the eigenvectors form an orthonormal basis. That just means that any vector can be built from a unique combination of 
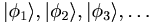, just like any vector in 3-D space can be built from a unique combination of x, y, and z, or any complex number can be built from 1 and i.
Contents |
Basics
Notation Definitions
From Linear Algebra
For All Vectors and Matrices
For Hermitian Operators
- UNIQ33152d511c2adb2a-math-0000000D-QINU
