Modern 2:Overview of Chapter 3

Overview of Chapter 3

 2/24/06 

Chapter 3 is all about measurement. Let's start with an idea from page 41 of the book:

repeatability of a measurement

If we measure a quantity A at some time t and find that the result is a, then we assume that if we measure this quantity again at a time just after t, we must get the same result. That means that in the second case the probability of getting a in the measurement was 1. In general that cannot be the case for the first measurment: there must be some range of possible outcomes of the measurement, each associated with some probability. The logical implication of this is that the measurement itself has transformed the system into a new state: it has been transformed into a state on which measurment of A gives a with certainty. Page 41 of the book.

This is a fundamental idea in QM and is sometimes referred to referred to as the collapse of the wavefunction. To understand what this means, we need some mathematical tools to help us define precisely what an observable quantity is and what are the results of measurements. The chapter begins with three ideas that are completely equivalent classically, but have rather different interpretations in QM.

key ideas on measurement

• The state of a system is system is described by a wavefunction. ψ(r,t). The wavefunction evolves deterministically according to the Schrodinger equation. However, we give a probabilistic interpretation to the wave function that allows us to predict the measurement of a given physical quantity.
• On the other hand, if we perform an experiment, the system will be in some state. How do we obtain as much information about this state.
• Finally, we may wish to perform an experiment on a system in a given state; i.e., one that is prepared experimentally to have well-defined properties.

But before we dive into this, we need to do a little mathematical preparation.

reminder from chapter 2

In position space we use 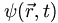$\psi(\vec{r},t)$ and we find the expected or most likely value of observables such as position by doing integrals of the form:

$\langle \vec{r} \rangle _ t = \int \vec{r} \ |\psi(\vec{r},t)|^2 d^3 r$

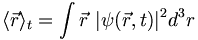
So far we've only encountered a few observables (position, momentum, energy). Then, if we had observables that were functions of momentum, we could perform the expectation calculations by going to momentum space, e.g.:

$\langle \vec{p} \rangle _ t = \int \vec{p} \ |\phi(\vec{p},t)|^2 d^3 p$

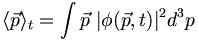
But we can also compute the expectation of p in position space. This is essential if we want to be able to treat variables such as angular momentum, which involve both position and momentum: 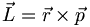$\vec{L} = \vec{r} \times \vec{p}$

Here is a fundamental result which you should prove:

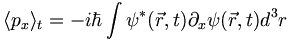
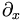(3.3) $\langle p _x \rangle _ t = -i \hbar \int \psi^*(\vec{r},t) \partial _x \psi(\vec{r},t) d^3 r$

$\partial _x$ means partial with respect to x. And henceforth, equation numbers such as 3.3 above will refer to the equation number in the text.

The general vector form of 3.3 is the following:

(3.4) $\langle \vec{p} \rangle _ t = -i \hbar \int \psi^*(\vec{r},t) \nabla \psi(\vec{r},t) d^3 r = \int \psi^*(\vec{r},t) \left( \hbar/i \nabla \right) \psi(\vec{r},t) d^3 r$

The reason I put brackets around the $\hbar /i \nabla$ is that we can consider this operator as being the position space representation of $\vec{p}$.

(3.9)   $\hbar /i  \nabla = \vec{p}$

Physical Quantities and Observables

vectors and operators

We're going to build up to the definition of an operator, but let's start with the idea of physical vectors. These are objects that have a direction and length (or magnitude). The force on an object for example. In a particular coordinate system we can represent this vector as a 3-tuple. E.g., 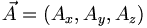$\vec{A} = (A_x, A_y, A_z)$. So the 3-tuple is the representation of the vector in a particular coordinate system. In other coordinates there will be other tuples, but the vector itself has an existance independent of the coordinates used.

So the way to think of a vector equation such as 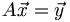$A \vec{x} = \vec{y}$ is that the object A is mapping one vector into another. If the vectors have the same length, then A can be represented by a square matrix. In the same way, we can think of functions as vectors too. Just as we add vectors component-wise:

$[\vec{x} + \vec{y}] _ i = x_i + y_i$

we add functions point-wise. If f and g are functions of one variable, then

[f + g](x) = f(x) + g(x)

The main difference between these two equations is that the functions, in effect, have an infinite number of components, one for each value of the real variable x!

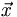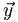Continuing this analogy, if we have two n-dimensional vectors $\vec{x}$ and $\vec{y}$ we take the dot-product or inner-product by summing the products of the individual components:

$\vec{x} \cdot \vec{y} \equiv (\vec{x},\vec{y}) = \sum _ {i=1} ^ n x_i y_y$

We will use this bracket notation all the time, so please focus on it. Now we can at least consider the possibility of having vectors with an infinite number of components. The main difficulty we would face is that whereas in a finite dimensional space any two vectors have a dot product, in an infinite dimensional space we have to consider whether or not the following infinite series actually converges:

$(\vec{x},\vec{y}) = \sum _ {i=1} ^ \infty x_i y_y$

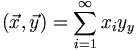
There is a suble difference between vectors that have an infinite number of components which we can lable by integers (denumerably infinite) and those where the number of components is continuously infinite, such as $f(x)$