Modern 2:Overview of Chapter 3
Contents |
Overview of Chapter 3
2/24/06
key ideas on measurement
- The state of a system is system is described by a wavefunction. ψ(r,t). The wavefunction evolves deterministically according to the Schrodinger equation. However, we give a probabilistic interpretation to the wave function that allows us to predict the measurement of a given physical quantity.
- On the other hand, if we perform an experiment, the system will be in some state. How do we obtain as much information about this state.
- Finally, we may wish to perform an experiment on a system in a given state; i.e., one that is prepared experimentally to have well-defined properties.
reminder from chapter 2
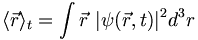
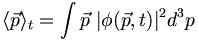
But we can also compute the expectation of p in position space. This is essential if we want to be able to treat variables such as angular momentum, which involve both position and momentum: 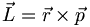
Here is a fundamental result which you should prove:
(3.3) 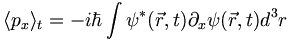
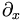 means partial with respect to x. And henceforth, equation numbers such as 3.3 above will refer to the equation number in the text.
means partial with respect to x. And henceforth, equation numbers such as 3.3 above will refer to the equation number in the text.
The general vector form of 3.3 is the following:
(3.4) 
The reason I put brackets around the  is that we can consider this operator as
being the position space representation of
is that we can consider this operator as
being the position space representation of 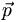 .
.
(3.9)
Physical Quantities and Observables
We're going to build up to the definition of an operator, but
let's start with the idea of physical vectors. These are objects that have a direction and length (or magnitude). The force on an object for example. In a particular coordinate system we can represent this vector as a 3-tuple. E.g., 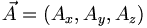 .
.