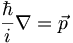Modern 2:Overview of Chapter 3
(→physical and abstract vectors) |
|||
| (5 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | {{Start Hierarchy|link=Course Wikis|title=Course Wikis}} |
| + | {{Hierarchy Item|link=Physics Course Wikis|title=Physics Course Wikis}} | ||
| + | {{Hierarchy Item|link=Modern 2|title=Modern 2}} | ||
| + | {{End Hierarchy}} | ||
| + | |||
2/24/06 | 2/24/06 | ||
| Line 6: | Line 10: | ||
==repeatability of a measurement== | ==repeatability of a measurement== | ||
| + | |||
| + | [http://mesoscopic.mines.edu/~jscales/320/fig2-3.gif statistical interpretation of repeated measurements] | ||
| + | |||
| + | |||
If we measure a quantity ''A'' at some time ''t'' and find that the result is ''a'', then we assume that if we measure this quantity again at a time just after ''t'', we must get the same result. That means that in the second case the probability of getting ''a'' in the measurement was 1. In general that cannot be the case for the first measurment: there must be some range of possible outcomes of the measurement, each associated with some probability. The logical implication of this is that the measurement itself has transformed the system into a new state: it has been transformed into a state on which measurment of '''''A'' gives ''a'' with certainty'''. Page 41 of the book. | If we measure a quantity ''A'' at some time ''t'' and find that the result is ''a'', then we assume that if we measure this quantity again at a time just after ''t'', we must get the same result. That means that in the second case the probability of getting ''a'' in the measurement was 1. In general that cannot be the case for the first measurment: there must be some range of possible outcomes of the measurement, each associated with some probability. The logical implication of this is that the measurement itself has transformed the system into a new state: it has been transformed into a state on which measurment of '''''A'' gives ''a'' with certainty'''. Page 41 of the book. | ||
| − | This is a fundamental idea in QM and is sometimes | + | This is a fundamental idea in QM and is sometimes referred to as the collapse of the wavefunction. To understand |
what this means, we need some mathematical tools to help us define precisely what an observable quantity is and what are the results of measurements. The chapter begins with three ideas that are completely equivalent classically, but have rather different interpretations in QM. | what this means, we need some mathematical tools to help us define precisely what an observable quantity is and what are the results of measurements. The chapter begins with three ideas that are completely equivalent classically, but have rather different interpretations in QM. | ||
| Line 42: | Line 50: | ||
The general vector form of 3.3 is the following: | The general vector form of 3.3 is the following: | ||
| − | '''(3.4)''' <math> \langle \vec{p} \rangle _ t = -i \hbar \int \psi^*(\vec{r},t) \nabla \psi(\vec{r},t) d^3 r = \int \psi^*(\vec{r},t) \left( \hbar | + | '''(3.4)''' <math> \langle \vec{p} \rangle _ t = -i \hbar \int \psi^*(\vec{r},t) \nabla \psi(\vec{r},t) d^3 r = \int \psi^*(\vec{r},t) \left( \frac{\hbar}{i} \nabla \right) \psi(\vec{r},t) d^3 r </math> |
| − | The reason I put brackets around the <math> \hbar | + | The reason I put brackets around the <math> \frac{\hbar}{i} \nabla </math> is that we can consider this operator as |
being the position space representation of <math>\vec{p}</math>. | being the position space representation of <math>\vec{p}</math>. | ||
| − | '''(3.9)''' <math> \ | + | '''(3.9)''' <math> \frac{\hbar}{i} \nabla = \vec{p} </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Latest revision as of 21:39, 13 March 2006
| Course Wikis | > | Physics Course Wikis | > | Modern 2 |
2/24/06
Chapter 3 is all about measurement. Let's start with an idea from page 41 of the book:
repeatability of a measurement
statistical interpretation of repeated measurements
If we measure a quantity A at some time t and find that the result is a, then we assume that if we measure this quantity again at a time just after t, we must get the same result. That means that in the second case the probability of getting a in the measurement was 1. In general that cannot be the case for the first measurment: there must be some range of possible outcomes of the measurement, each associated with some probability. The logical implication of this is that the measurement itself has transformed the system into a new state: it has been transformed into a state on which measurment of A gives a with certainty. Page 41 of the book.
This is a fundamental idea in QM and is sometimes referred to as the collapse of the wavefunction. To understand what this means, we need some mathematical tools to help us define precisely what an observable quantity is and what are the results of measurements. The chapter begins with three ideas that are completely equivalent classically, but have rather different interpretations in QM.
key ideas on measurement
- The state of a system is system is described by a wavefunction. ψ(r,t). The wavefunction evolves deterministically according to the Schrodinger equation. However, we give a probabilistic interpretation to the wave function that allows us to predict the measurement of a given physical quantity.
- On the other hand, if we perform an experiment, the system will be in some state. How do we obtain as much information about this state.
- Finally, we may wish to perform an experiment on a system in a given state; i.e., one that is prepared experimentally to have well-defined properties.
But before we dive into this, we need to do a little mathematical preparation.
reminder from chapter 2
In position space we use 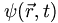 and we find the expected or most likely value of observables such as position by doing integrals of the form:
and we find the expected or most likely value of observables such as position by doing integrals of the form:
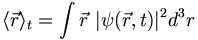
So far we've only encountered a few observables (position, momentum, energy). Then, if we had observables that were functions of momentum, we could perform the expectation calculations by going to momentum space, e.g.:

But we can also compute the expectation of p in position space. This is essential if we want to be able to treat variables such as angular momentum, which involve both position and momentum: 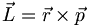
Here is a fundamental result which you should prove:
(3.3) 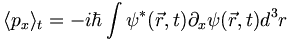
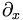 means partial with respect to x. And henceforth, equation numbers such as 3.3 above will refer to the equation number in the text.
means partial with respect to x. And henceforth, equation numbers such as 3.3 above will refer to the equation number in the text.
The general vector form of 3.3 is the following:
(3.4) 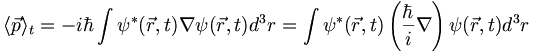
The reason I put brackets around the 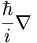 is that we can consider this operator as
being the position space representation of
is that we can consider this operator as
being the position space representation of 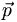 .
.
(3.9)