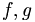Modern 2:Operators, Observables, and Measurment

Course Wikis

>

Physics Course Wikis

>

Modern 2

Operators, Observables, and Measurement

physical and abstract vectors

We're going to build up to the definition of an operator, but let's start with the idea of physical vectors. These are objects that have a direction and length (or magnitude). The force on an object for example. In a particular coordinate system we can represent this vector as a 3-tuple. E.g., 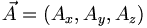$\vec{A} = (A_x, A_y, A_z)$. So the 3-tuple is the representation of the vector in a particular coordinate system. In other coordinates there will be other tuples, but the vector itself has an existance independent of the coordinates used.

So the way to think of a vector equation such as 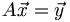$A \vec{x} = \vec{y}$ is that the object A is mapping one vector into another. If the vectors have the same length, then A can be represented by a square matrix. In the same way, we can think of functions as vectors too. Just as we add vectors component-wise:

$[\vec{x} + \vec{y}] _ i = x_i + y_i$

we add functions point-wise. If f and g are functions of one variable, then

$[f + g](x) = f(x) + g(x) \$

The main difference between these two equations is that the functions, in effect, have an infinite number of components, one for each value of the real variable x!

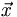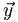Continuing this analogy, if we have two n-dimensional vectors $\vec{x}$ and $\vec{y}$ we take the dot-product or inner-product by summing the products of the individual components:

$\vec{x} \cdot \vec{y} \equiv (\vec{x},\vec{y}) = \sum _ {i=1} ^ n x_i y_i$

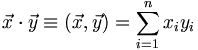
We will use this bracket notation all the time, so please focus on it. Now we can at least consider the possibility of having vectors with an infinite number of components. The main difficulty we would face is that whereas in a finite dimensional space any two vectors have a dot product, in an infinite dimensional space we have to consider whether or not the following infinite series actually converges:

$(\vec{x},\vec{y}) = \sum _ {i=1} ^ \infty x_i y_i$

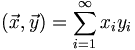
So, how do you suppose we should define the dot product of two continuous functions? Assume we have two real functions defined on the entire real line. Then, assuming the integral converges, we would say:

$(f,g) = \int _ {-\infty} ^ {\infty} f(x) g(x) dx$

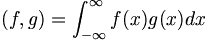
If the functions are complex valued then we need to put a complex conjugate in the definition of the inner product in order that 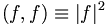$(f,f) \equiv |f|^2$ be real:

$(f,g) = \int _ {-\infty} ^ {\infty} f^*(x) g(x) dx$

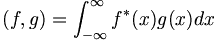
There is a suble difference between vectors that have an infinite number of components which we can lable by integers (countably infinite) and those where the number of components is continuously infinite, such as f(x)

Here is what Mathworld says:

countably infinite uncountably infinite. See also the definition of continuum

These more general sets of vectors all satisfy the formal mathematical definition of vector spaces.  

A linear vector space over a set F of scalars is a set of elements V together with a function called addition from 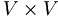$V \times V$ into V and a function called scalar multiplication from 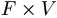$F \times V$ into V satisfying the following conditions for all 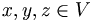$x,y,z \in V$ and all $\alpha, \beta \in F$:

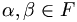• [V1:] (x + y) + z = x + (y + z)
• [V2:] x + y = y + x
• [V3:] There is an element 0 in V such that x + 0 = x for all $x \in V$.
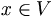• [V4:] For each 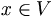$x \in V$ there is an element 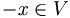$-x \in V$ such that x + ( − x) = 0.
• [V5:] α(x + y) = αx + αy
• [V6:] (α + β)x = αx + βx
• [V7:] α(βx) = (αβ)x
• [V8:] $1 \cdot x = x$

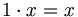
operators

An operator maps a vector into a vector. Henceforth we will use the general definition of a vector. Wavefunctions are examples of vectors. So an operator equation would be of the form

$A f(x) = g(x) \,$

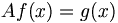
We will only deal with linear operators in this course. This means that any such operator satisfies:

$A(f(x) + g(x)) = Af(x) + Ag(x) \,$

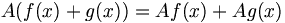
Hermetian operators or matrices

The transpose of a matrix A is denoted by A^T and is defined as follows: the i,j components of A^T are equal to the j,i components of A.

The Hermitian conjugate or adjoint of a matrix is the complex conjugate of the transpose. This is denoted A^H (H for Hermitian conjugate). When referring to operators, the adjoint is sometimes denoted by a dagger instead of an H: 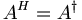$A^H = A^{\dagger}$. For our purposes we will treat these notations as indistinguishable. A matrix that is equal to its Hermitian conjugate is said to be a Hermitian matrix, or self-adjoint.

Now, referring back to our definition of the inner product of two complex functions:

$(f,g) = \int _ {-\infty} ^ {\infty} f^*(x) g(x) dx$

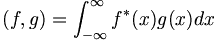
The book uses a hat on top of a upper case roman letter to refer to operators, so let 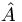$\hat{A}$ be an operator. Then if the operator is self-adjoing, or Hermitian,

$(\hat{A}f,g) = \int \left[ \hat{A} f\right] ^* g \ d^3 r = \int f^* \left[\hat{A} g\right] d^3r = (f,\hat{A} g)$ for any pair of functions $f, g \,$