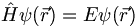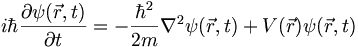Modern 2:More on Eigenfunctions and Measurements

Course Wikis

>

Physics Course Wikis

>

Modern 2

I think I can safely say that no one understands quantum mechanics. -- R.P. Feynman

Notice the Dirac bra-kets on the blackboard.

More on the time/energy uncertainty relation

In quantum mechanics time plays a fundamentally different role than other observables. It is not an operator, like position and momentum, it is a parameter which incrases during the course of experiments. We are conscious not so much of time itself but of the passage of time. If I showed you two apparently identical photographs of an outdoor scene take exactly one year apart under identical lighting conditions, you would not know that a year had passed. But if I showed you the same scene in winter and summer, the passage of time would be clear.

Conisder the official definition of time from the BIPM

The second is the duration of 9 192 631 770 periods of the radiation corresponding 
to the transition between the two hyperfine levels of the ground state of the 
caesium 133 atom.

In other words, the frequency of the photons which are resonant with this transition in the ground state of Cs is exactly 9192631770 Hz = 9.192631770 GHz

ultra narrow spectra in a modern atomic clock

The key idea is: the longer the lifetime of an excited state, the narrower its spectral line. Mathematica notebook on time/frequency uncertainty for Gaussians

Mathematica notebook on chirps, a classical example of time/frequency uncertainty

But what we really measure is not time at all, it's frequency.

Never measure anything but frequency:  Arthur Schawlow 

Shawlow was the co-inventor of the laser and got the Nobel Prize in 1981. Schawlow's very interesting Nobel lecture

Rest of the class: solve Schrodinger for simple potentials

Run the following applets on the CD that came with your book: 1.2, 1.4, 2.1, 2.2

From the previous lecture:

Here is the Schrodinger equation for a nonrelativistic particle in an external, time-independent potential

$i \hbar \frac{\partial \psi(\vec{r}, t)}{\partial t} = - \frac{\hbar^2}{2 m} \nabla^2 \psi(\vec{r}, t) + V(\vec{r}) \psi(\vec{r}, t)$

In the homework you will prove that the position-space represnetation of the momentum operator is given by

(3.9) 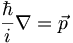$\frac{\hbar}{i} \nabla = \vec{p}$

I'm going to rewrite this using a hat over the momentum to indicate the fact that it is really an operator:

$\frac{\hbar}{i} \nabla = \hat{\mathbf{p}}$

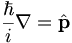
Let us define an operator for the total energy (kinetic plus potential). This is called the Hamiltonian

$\hat{H} = \frac{{\hat{\mathbf{p}}}^2}{2m} + \hat{V}$

$= - \frac{\hbar^2}{2 m} \nabla^2 + V(\vec{r})$

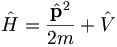
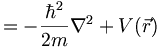
Using this we can rewrite the Schrodinger equation as

(3.16)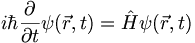 $i \hbar \frac{\partial}{\partial t} \psi(\vec{r}, t) = \hat{H} \psi(\vec{r}, t)$

Normally we expect that the result repeated measurments of systems prepared identically will yield a spread of results. But there are clearly some measurement which lead to very precise and repeatable measurements, such as spectral lines, narrow-band laser frequencies, etc. So let us consider the case in which the time dependence of the wave function is a constant frequency sinusoid. I.e., suppose that

$\psi(\vec{r},t) = \psi(\vec{r}) e^{-i \omega t} = \psi(\vec{r}) e^{-i E t/ \hbar}$

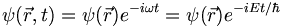
A constant frequency means a constant energy. So if we plug this kind of wavefunction into 3.16 the Schrodinger equation becomes

 (3.17) $\hat{H} \psi(\vec{r}) = E \psi(\vec{r})$