Modern 2:Evolution of Wavepackets

Course Wikis

>

Physics Course Wikis

>

Modern 2

Evolution of Wavepackets

The Schroedinger Equation is first order in time:

$i \hbar \frac{\partial \psi(\vec{r}, t)}{\partial t} = - \frac{\hbar^2}{2 m} \nabla^2 \psi(\vec{r}, t)$

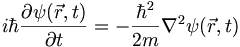
This means that the wavefunction at any time is completely determined by its value at an earlier time.

Consider a generic first order (in time) differential equation written in operator form:

$\frac{\partial \psi(\vec{r}, t)}{\partial t} = - H \psi(\vec{r}, t)$

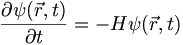
Where H is a differential operator (such as 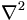$\nabla^2$) that does not depend on time. A solution of this equation is given by:

$\psi(\vec{r}, t) = e^{-H t} \psi(\vec{x}, 0)$

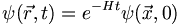
The operator e ^{− Ht} can be thought of as an evolution operator since it evolves the wavefunction forward in time. NB, there is nothing special about t = 0. We can give the initial conditions at any time then by shifting the time axis, this becomes t = 0. This would be an extremely handy tool to be able to apply to the Schroedinger equation but we have to figure out how to deal with the exponential of a differential operator.

The simplest approach is to Fourier transform the spatial part of the Schroedinger equation:

$\nabla^2 \rightarrow (i \vec{k})^2$

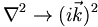
In case you're shakey on this argument...

Suppose we have a first order equation:

$\frac{\partial f(x,t)}{\partial t} = \frac{\partial f(x,t)}{\partial x}$

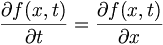
We know that

$f(x,t) = \frac{1}{\sqrt{2 \pi}} \int g(k, t) e^{i k x} \, dk$

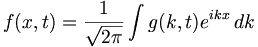
Hence differentiating this with respect to t and x and using Equation 1 we have:

$\frac{1}{\sqrt{2 \pi}} \int \frac{\partial g(k,t)}{\partial t} e^{i k x} \, dk = \frac{1}{\sqrt{2 \pi}} \int g(k, t) (i k) e^{i k x} \, dk$

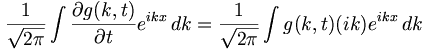
Thus

$\frac{1}{\sqrt{2 \pi}} \int \left[ \frac{\partial g(k,t)}{\partial t} - (i k) g(k, t) \right] e^{i k x} \, dk = 0$

The only way this can be true in general is for the quantity in the square brackets to be zero. This leaves, in effect, the Fourier Transform of Equation 1:

$\frac{\partial g(k,t)}{\partial t} = i k g(k, t)$

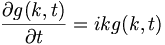
So, in practice we can replace space derivatives with multiplaction by i k in the wavenumber (momentum) domain. For vectors this generalizes in a completely natural way. Gradients become multiplication by 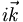$i \vec{k}$, and the Laplacian $\nabla^2 \rightarrow (i \vec{k})^2$.

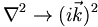Now back to Schroedinger... In the wavenumber domain we have:

$i \hbar \frac{\partial \psi(\vec{k}, t)}{\partial t} = - \frac{\hbar^2}{2 m} (i \vec{k})^2 \psi(\vec{k},t)$

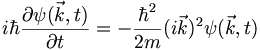
which gives the nice evolution equation:

$\frac{\partial \psi(\vec{k}, t)}{\partial t} = - i \frac{\hbar}{2 m} \vec{k}^2 \psi(\vec{k},t)$

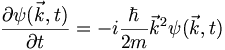
Hence the evolution operator can be written via:

$\psi(\vec{k}, t) = e^{- i \hbar k^2 t/{2 m}} \psi(\vec{k}, 0)$

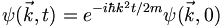
The exponent of this expression can be written as well in terms of momentum 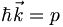$\hbar \vec{k} = p$ or energy (for a free particle) $E = \frac{p^2}{2 m}$.

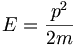A slight digression...

Another approach to computing the exponential of an operator (e.g. a matrix) is to make a Taylor series expansion of the exponential. We have

e^x = 1 + x + x² + ...

So it's at least plausible that we could define the exponential of an operator as

e^A = 1 + A + A² + ...

where an expression such as A² really means to apply the operator A twice to some object in its domain of definition; something like A(A(f)).