Homework 1
From Physiki
(Difference between revisions)
(New page: == Sets == # Given sets <math>A</math> and <math>B</math>, show that <math>A \cap B</math> is the largest common subset of <math>A</math> and <math>B</math>, in the sense that it contain...) |
|||
| Line 1: | Line 1: | ||
== Sets == | == Sets == | ||
| − | # Given sets <math>A</math> and <math>B</math>, show that <math>A \cap B</math> is the largest common subset of <math>A</math> and <math>B</math>, in the sense that it contains every such common subset. | + | # <p>Given sets <math>A</math> and <math>B</math>, show that <math>A \cap B</math> is the largest common subset of <math>A</math> and <math>B</math>, in the sense that it contains every such common subset.<br>Note: Typically for statements involving ''largest'' or ''smallest'', a proof by contradiction works quite well.</p> |
| − | + | # Given sets <math>A</math> and <math>B</math>, prove if <math>A \cap X = B \cap X</math> and <math>A \cup X = B \cup X</math> for some set X, then <math>A = B</math><br>Hint: <math>A = A \cap (A \cup X)</math> | |
| − | + | ||
| − | + | ||
| − | # Given sets <math>A</math> and <math>B</math>, prove if <math>A \cap X = B \cap X</math> and <math>A \cup X = B \cup X</math> for some set X, then <math>A = B</math> | + | |
| − | + | ||
== Functions == | == Functions == | ||
| − | # Given functions <math>f:A \rightarrow B</math> and <math>g:B \rightarrow C</math>, prove that if <math>g \circ f</math> is one-to-one (injective), then <math>f</math> is one-to-one. | + | # Given functions <math>f:A \rightarrow B</math> and <math>g:B \rightarrow C</math>, prove that if <math>g \circ f</math> is one-to-one (injective), then <math>f</math> is one-to-one.<br>Note: The function <math>g</math> need not be injective nor surjective. |
| − | Note: The function <math>g</math> need not be injective nor surjective. | + | # Consider a circle C, a straight line tangent to it L, and a point P located anywhere in the plane of the circle except on L. Define the mapping <math>f:C \rightarrow L</math> by a point <math>c_1 \in C</math> is mapped to a point <math>l_1 \in L</math> if and only if they are collinear with P, i.e. a straight line passes through <math>c_1, l_1 \text{ and } P</math>. Consider this mapping for each of the following locations of P and answer the following questions: Is f a function and if so, is it injective, surjective, and/or bijective? |
| + | ## P may lie anywhere on the opposite side of the line from C. | ||
| + | ## P lies on the same side of the line as the circle but outside the circle. | ||
| + | ## P is inside the circle | ||
| + | ## P lies on the circle but not diametrically opposite the point of tangency. | ||
| + | ## P lies on the circle diametrically opposite the point of tangency. | ||
| + | |||
| + | == Equivalences == | ||
| + | |||
| + | # Let f be a function mapping set A into set B. Define the relation <math>\rho</math> on A by<br> <math>x \rho y \leftrightarrow f(x) = f(y)</math>.<br> Show that <math>\rho</math> is an equivalence relation on A and define the corresponding equivalence classes.<br>Note: <math>\rho</math> is called the ''kernel equivalence of f''. | ||
| + | |||
| + | == Numbers == | ||
| + | |||
| + | # Find the gcd(198,241) and express it as a linear combination of 198 and 241. | ||
| + | |||
| + | == Binary Operations == | ||
| − | # | + | # On<math>\mathbb{Z}^+</math>, define <math>a * b = c</math> where c is the largest integer less than the product of a and b. Determine if * is a binary operation and if not, why it fails. |
| − | # | + | # Suppose that * is an associative binary operation on a set S. Let <math>H = \{a \in S | a*x = x*a \text{ for all } x \in S\}</math>. Show that H is closed under *. |
Latest revision as of 20:02, 17 January 2008
Contents |
Sets
-
Given sets A and B, show that
is the largest common subset of A and B, in the sense that it contains every such common subset.
Note: Typically for statements involving largest or smallest, a proof by contradiction works quite well. - Given sets A and B, prove if
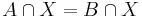and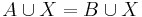 
for some set X, then A = B
Hint: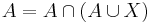
Functions
- Given functions
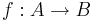and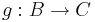 
, prove that if 
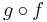is one-to-one (injective), then f is one-to-one.
Note: The function g need not be injective nor surjective. - Consider a circle C, a straight line tangent to it L, and a point P located anywhere in the plane of the circle except on L. Define the mapping
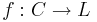by a point 
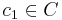is mapped to a point 
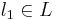if and only if they are collinear with P, i.e. a straight line passes through c1,l1 and P. Consider this mapping for each of the following locations of P and answer the following questions: Is f a function and if so, is it injective, surjective, and/or bijective?
- P may lie anywhere on the opposite side of the line from C.
- P lies on the same side of the line as the circle but outside the circle.
- P is inside the circle
- P lies on the circle but not diametrically opposite the point of tangency.
- P lies on the circle diametrically opposite the point of tangency.
Equivalences
- Let f be a function mapping set A into set B. Define the relation ρ on A by
.
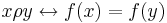Show that ρ is an equivalence relation on A and define the corresponding equivalence classes.
Note: ρ is called the kernel equivalence of f.
Numbers
- Find the gcd(198,241) and express it as a linear combination of 198 and 241.
Binary Operations
- On
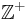, define a * b = c where c is the largest integer less than the product of a and b. Determine if * is a binary operation and if not, why it fails.
- Suppose that * is an associative binary operation on a set S. Let
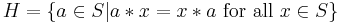. Show that H is closed under *.
