HW 8
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | 1) The Fourier series of a Sin function should be trivial, right? Execute the following Mathematica code. Explain the result. | + | 1) The Fourier series of a Sin function should be trivial, right? Execute the following Mathematica code. Explain the result. |
FourierTrigSeries[Sin[x], x, 4] | FourierTrigSeries[Sin[x], x, 4] | ||
Remember to load the appropriate library before you try this. | Remember to load the appropriate library before you try this. | ||
| − | 2) Look at problem 5.2 in Chapter 7 of Boas. Verify the first nonzero Sin and Cosine terms by doing the integrals by hand. Then show | + | 2) Look at problem 5.2 in Chapter 7 of Boas. Verify the first nonzero Sin and Cosine terms by doing the integrals by hand. Then show the precise call to FourierTrigSeries that will reproduce the 8 terms shown in the answer. This will require to look carefully into the definitions used by Mathematica and the optional arguments of FourierTrigSeries. |
3-4) Chapter 7, section 10 of Boas: Problems 4 and 9. | 3-4) Chapter 7, section 10 of Boas: Problems 4 and 9. | ||
5) Prove Equation 11.5 on page 375. | 5) Prove Equation 11.5 on page 375. | ||
| + | |||
| + | 6) Show that this function is ''normalized''. That means that when you integrate it from | ||
| + | -infinity to +infinity you get 1: | ||
| + | |||
| + | <math>\frac{1}{\sqrt{2 \pi} \sigma} e^{(-(t - m)^2/(2 \sigma^2))} </math> | ||
| + | |||
| + | 7) Show that the Fourier transform of this function is: | ||
| + | <math>\frac{e^{i m w-\frac{w^2 \sigma ^2}{2}}}{\sqrt{2 \pi }}</math> | ||
| + | |||
| + | Thus, the Fourier transform of a Gaussian is not a Gaussian itself unless the mean is zero. | ||
Latest revision as of 19:21, 28 October 2007
1) The Fourier series of a Sin function should be trivial, right? Execute the following Mathematica code. Explain the result.
FourierTrigSeries[Sin[x], x, 4]
Remember to load the appropriate library before you try this.
2) Look at problem 5.2 in Chapter 7 of Boas. Verify the first nonzero Sin and Cosine terms by doing the integrals by hand. Then show the precise call to FourierTrigSeries that will reproduce the 8 terms shown in the answer. This will require to look carefully into the definitions used by Mathematica and the optional arguments of FourierTrigSeries.
3-4) Chapter 7, section 10 of Boas: Problems 4 and 9.
5) Prove Equation 11.5 on page 375.
6) Show that this function is normalized. That means that when you integrate it from -infinity to +infinity you get 1:
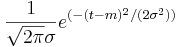
7) Show that the Fourier transform of this function is:
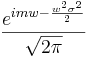
Thus, the Fourier transform of a Gaussian is not a Gaussian itself unless the mean is zero.