Classical vs quantum harmonic oscillator. Correspondance principle

(Difference between revisions)
Jump to: navigation, search
(→Now let's look at some of the quantum harmonic oscillator states)
(→Now let's look at some of the quantum harmonic oscillator states)
Line 86: Line 86:
 
With <math>E_n = (n + 1/2) \hbar \omega</math>.  To make the classical correspondance, we want:
 
With <math>E_n = (n + 1/2) \hbar \omega</math>.  To make the classical correspondance, we want:
  
−
<math> 1/2 K A ^2 = (n + 1/2) \hbar \omega</math>.  Hence to get a classical oscillator with the same energy as the quantum oscillator we choose:
+
<math> \frac{1}{2} K A ^2 = (n + 1/2) \hbar \omega</math>.  Hence to get a classical oscillator with the same energy as the quantum oscillator we choose:
  
 
<math>A^2 = 2 (n + 1/2) \hbar \omega / (m \omega ^2) =  2 (n + 1/2) \hbar /(m \omega) </math>.  But remember,  <math>\hbar /(m \omega)</math>
 
<math>A^2 = 2 (n + 1/2) \hbar \omega / (m \omega ^2) =  2 (n + 1/2) \hbar /(m \omega) </math>.  But remember,  <math>\hbar /(m \omega)</math>

Revision as of 18:37, 31 March 2006

Contents

reminder: Jared Diamond talk next tuesday

[talk announcement]

some key ideas on the harmonic oscillator

  • ω is the natural frequency of the oscillator. This

is a property of the potential. Remember, for small displacements from equilibrium: x0.

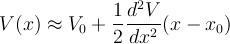
V(x) \approx V_0 + \frac{1}{2}\frac{d^2 V}{dx^2} (x - x_0)

Hence the force associatd with the potential is:

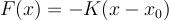
F(x) = - K (x - x_0) \

where 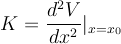K = \frac{d^2 V}{dx^2} |_{x=x_0}

  • in 1D the QHO has an infinite series of equally spaced energy levels:

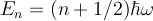
E_n = (n + 1/2) \hbar \omega

  • many of the calculations become simpler if we introduce dimensionless variables

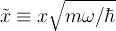
\tilde{x} \equiv x \sqrt{m \omega/\hbar}

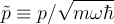
\tilde{p} \equiv p /\sqrt{m \omega \hbar}

In particular, you can show that:

Variance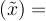( \tilde{x}) = Variance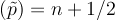( \tilde{p}) = n + 1/2

This is a striking result since it says that for energy eigenstates, nature will not allow us to sacrafice knowledge of one variable, in order to gain knowledge of the other.

Brief digression, the astounding cancelation properties of Hermite polynomials

Mathematica.png Download try this yourself

Classical versus Quantum harmonic oscillator

We've seen two ways to write the equations of motion for the classical SHO: 

Newtonian: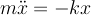   m \ddot{x} = - k x  

Hamiltonian: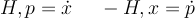   H,p = \dot{x}  \ \ \ \ -H,x = \dot{p}

where 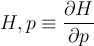H,p \equiv \frac{\partial H}{\partial p}

In either case, the solution is:

x(t) = A \cos(\omega _0 t + \Delta) \ where \Delta \ is a phase factor.

Now, from this solution it is not hard to show that the total energy is a constant:

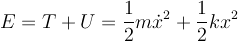
E = T + U = \frac{1}{2} m \dot{x} ^2 + \frac{1}{2} k x^2

Hence, 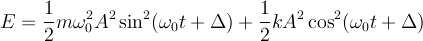E = \frac{1}{2} m \omega_0 ^2 A ^2 \sin^2(\omega _0 t + \Delta) + \frac{1}{2} k A ^2 \cos^2(\omega _0 t + \Delta)

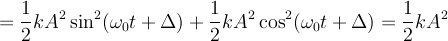
= \frac{1}{2} k A ^2 \sin^2(\omega _0 t + \Delta) + \frac{1}{2} k A ^2 \cos^2(\omega _0 t + \Delta) =\frac{1}{2} k A^2

So, in the classical case (assuming no dissipation) we adjust the energy by adjusting how far we pull the mass from its equilibrium position. Once we've done that, it oscillates in simple harmonic motion forever.


Where does the mass-on-a-spring spend most of its time

Mathematica.png Download SHO motion

Now let's look at some of the quantum harmonic oscillator states

Mathematica.png Download several harmonic oscillator eigenstates 
Key idea:  for small n, the mass is most likely to be near x=0.  This is exactly the opposite of the classical case.

However, for large n, the classical and quantum result are similar, with a few exceptions.

  • There are still nodes in

the probability due to the interference of the back and forth wave-like propagation of the particle.

  • The limit of the classical motion is strictly 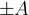\pm A. However, there is small but nonzero that

the quantum particle will be found outside this limit. This is another example of tunneling.


With 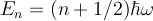E_n = (n + 1/2) \hbar \omega. To make the classical correspondance, we want:

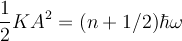\frac{1}{2} K A ^2 = (n + 1/2) \hbar \omega. Hence to get a classical oscillator with the same energy as the quantum oscillator we choose:

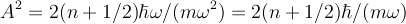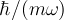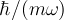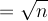A^2 = 2 (n + 1/2) \hbar \omega / (m \omega ^2) = 2 (n + 1/2) \hbar /(m \omega) . But remember, \hbar /(m \omega) is our basic unit of length (which we used to make the equations dimensionless). Hence in units of \hbar /(m \omega) we want the amplitude of our classical spring to be = \sqrt n (ignoring the small factor of 1/2.

the correspondance principle

As n gets large, the quantum problem approaches the classical

Or, another way to think of this is: when is the discreteness of the energy levels, 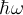\hbar \omega , small enough to be ignored.

Other examples include Rydberg states for atoms. These are highly excited states with nearly spherical orbits.

Retrieved from "http://inksurvey.org/csm/wiki/index.php?title=Classical_vs_quantum_harmonic_oscillator._Correspondance_principle&oldid=830"
Personal tools
Namespaces
Variants
Actions
Navigation
Toolbox