Classical vs quantum harmonic oscillator. Correspondance principle

(Difference between revisions)

Jump to: navigation, search

Revision as of 15:10, 31 March 2006

some key ideas on the harmonic oscillator

$ω /$ is the natural frequency of the oscillator. This

is a property of the potential. Remember, for small displacements from equilibrium: $x 0$ .

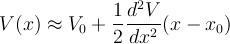
$V(x) \approx V_0 + \frac{1}{2}\frac{d^2 V}{dx^2} (x - x_0)$

Hence the force associatd with the potential is:

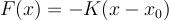
$F(x) = - K (x - x_0) \$

where 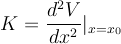$K = \frac{d^2 V}{dx^2} |_{x=x_0}$

in 1D the QHO has an infinite series of equally spaced energy levels:

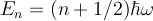
$E_n = (n + 1/2) \hbar \omega$

many of the calculations become simpler if we introduce dimensionless

variables

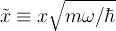
$\tilde{x} \equiv x \sqrt{m \omega/\hbar}$

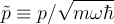
$\tilde{p} \equiv p /\sqrt{m \omega \hbar}$

In particular, you can show that:

Variance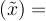 $( \tilde{x}) =$ Variance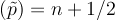 $( \tilde{p}) = n + 1/2$

This is a striking result since it says that for energy eigenstates, nature will not allow us to sacrafice knowledge of one variable, in order to gain knowledge of the other.

Brief digression, the astounding cancelation properties of Hermite polynomials

Download try this yourself

Classical versus Quantum harmonic oscillator

Here are

@@ Line 33: / Line 33: @@
 ===Brief digression, the astounding cancelation properties of Hermite polynomials===
-{{mathematica|filename=Hermite_cancelation.nb|title=try this yourself}}
+{{mathematica|filename=Hermitecancelation.nb|title=try this yourself}}
 ===Classical versus Quantum harmonic oscillator ===

Classical vs quantum harmonic oscillator. Correspondance principle

Revision as of 15:10, 31 March 2006

some key ideas on the harmonic oscillator

Brief digression, the astounding cancelation properties of Hermite polynomials

Classical versus Quantum harmonic oscillator

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Toolbox