Bound states, scattering states. Examples. The harmonic oscillator
(Difference between revisions)
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| Line 17: | Line 12: | ||
<math> \Delta V = V'' \Delta x \ </math> to second order. This quadratic potential is called '''harmonic''' | <math> \Delta V = V'' \Delta x \ </math> to second order. This quadratic potential is called '''harmonic''' | ||
becuase the restoring force is linear: hence the particle executes simple harmonic motion when slightly perturbed from equilibrium. | becuase the restoring force is linear: hence the particle executes simple harmonic motion when slightly perturbed from equilibrium. | ||
| + | |||
| + | |||
| + | |||
| + | ==some examples of potentials== | ||
| + | |||
| + | [[Image:Boundstates.png]] | ||
Revision as of 16:02, 15 March 2006
small displacements from equilibrium
Consider "particles" connected by some attractive potential in equilibrium:
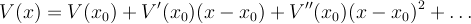
At equilibrium,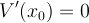 
, so
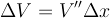to second order. This quadratic potential is called harmonic
becuase the restoring force is linear: hence the particle executes simple harmonic motion when slightly perturbed from equilibrium.
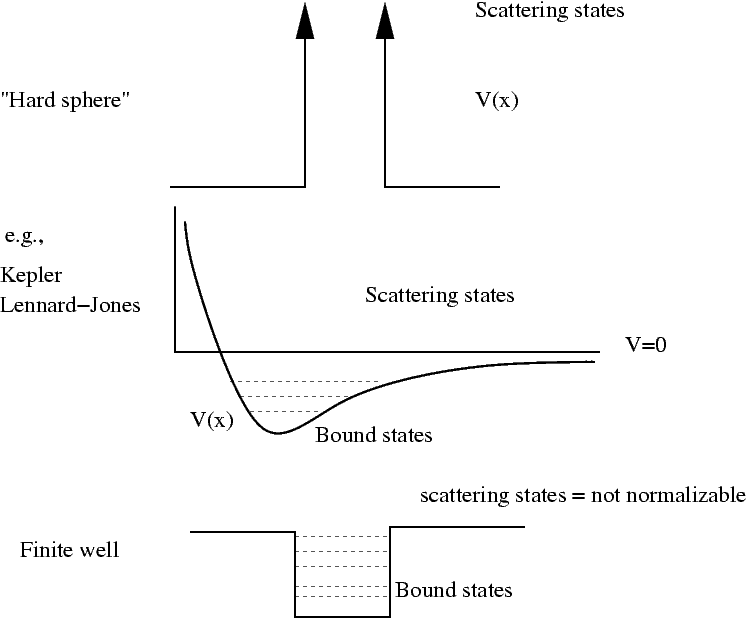
some examples of potentials
Regions that do not contain a well
- There are eigenfunctions for
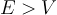. These eigenfunctions, however, are plane waves and are not square integrable. They cannot represent a single particle, but can represent a constant flux of particles. We calculate transmission and reflection coefficients by comparing fluxes.
Regions that do contain a well
- There exists an eigenfunction for every
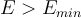. These eigenfunctions are not square integrable.
- For
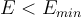eigenfunctions exist only for selected eigenvalues. For the finite square well potential we solve for these eigenvalues numerically.
