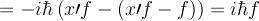Exam 2, more harmonic oscillators
| (20 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| + | ===test 2=== | ||
| + | |||
| + | * problem 1 | ||
| + | |||
<math> \frac{- \hbar ^2}{2m} \frac{d^2}{dx^2} \psi(x) = E \psi(x) </math> | <math> \frac{- \hbar ^2}{2m} \frac{d^2}{dx^2} \psi(x) = E \psi(x) </math> | ||
| Line 4: | Line 8: | ||
Inside the well we should expect plane wave solutions: | Inside the well we should expect plane wave solutions: | ||
| + | |||
<math>\psi(x) = A e^{i k x} + B e^{-ikx} \ </math> | <math>\psi(x) = A e^{i k x} + B e^{-ikx} \ </math> | ||
| + | |||
| + | Where <math> k^2 = \frac{2m}{\hbar ^2} E \ </math> | ||
Applying the BC this gives: | Applying the BC this gives: | ||
| Line 40: | Line 47: | ||
So we have two families of solutions: | So we have two families of solutions: | ||
| − | <math> \psi(x) = A \left(e^{i k x} + e^{-ikx} \right) = A \cos( \frac{2 \pi (n-1/2)}{a} x) \ </math> | + | <math> \psi(x) = A \left(e^{i k x} + e^{-ikx} \right) = A \cos \left( \frac{2 \pi (n-1/2)}{a} x \right) \ </math> |
| + | |||
| + | |||
| + | <math> \psi(x) = B \left(e^{i k x} - e^{-ikx} \right) = B \sin \left(\frac{2 \pi n}{a} x \right) \ </math> | ||
| + | |||
| + | |||
| + | The cosine states are even (have even parity), the sine states are odd (have odd parity) | ||
| + | |||
| + | Now since <math> k^2 = \frac{2m}{\hbar ^2} E \ </math> we have | ||
| + | |||
| + | <math> E_n = \frac{\hbar^2}{2m} \left( \frac{2}{a} \right) ^2 (2 n \pi)^2 = \xi 4(n-1/2)^2 \ </math> | ||
| + | for the odd parity states and | ||
| + | |||
| + | |||
| + | <math> E_n = \frac{\hbar^2}{2m} \left(\frac{2}{a} \right)^2 (2 (n- 1/2) \pi)^2 = \xi 4 n^2 \ </math> | ||
| + | for the even parity states. | ||
| + | |||
| + | |||
| + | In numerical order these are: | ||
| + | |||
| + | |||
| + | <math> \xi \times \{ 1, 4, 9, 16, ... \} </math> | ||
| + | |||
| + | |||
| + | * problem 5 | ||
| + | |||
| + | <math> [x,p_x] \ </math> is an operator equation. By definition it is: | ||
| + | <math> (x p_x - p_x x) \ </math>. In order to work this out it is helpful to apply the operator to a test function. | ||
| + | |||
| + | <math> [x,p_x] f(x) = (x p_x - p_x x)f(x) = (x (-i \hbar d/dx)) f(x) - ((-i \hbar d/dx) x) f(x) </math> | ||
| + | <math> = -i \hbar \left( x \prime{f} - (x \prime{f} - f) \right) = i \hbar f </math> | ||
| + | |||
| + | |||
| − | + | [[more on harmonic oscillators]] | |
Latest revision as of 16:20, 29 March 2006
test 2
- problem 1
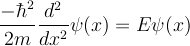
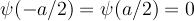
Inside the well we should expect plane wave solutions:
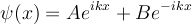
Where 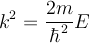
Applying the BC this gives:
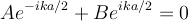
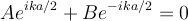
At this point you have two equatins and two unknowns. I don't care how you solve them. Here is one way. Add the two equations to get:
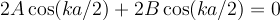
now subtract to get:
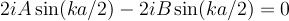
These are nice since we can factor out the common sine and cosine terms:
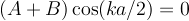
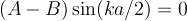
There are only two ways we can satisfy both equations simultaneously. If A=B then the second equatino is
taken care of, but then A+B cannot = 0, so we have to insist that 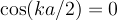 . This requires
. This requires
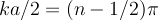
On the other hand, if we choose A = -B, then the first equation is automatically satisfied and then we must
insist that 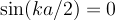 . This requires
. This requires
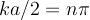
So we have two families of solutions:
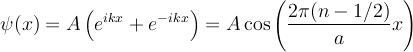
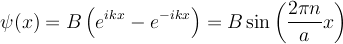
The cosine states are even (have even parity), the sine states are odd (have odd parity)
Now since 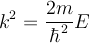 we have
we have
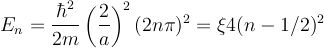 for the odd parity states and
for the odd parity states and
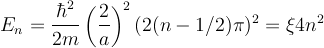 for the even parity states.
for the even parity states.
In numerical order these are:
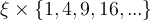
- problem 5
![[x,p_x] \](/csm/wiki/images/math/0/e/2/0e28cc64a7a48ad98ec0d676ec36201d.png) is an operator equation. By definition it is:
is an operator equation. By definition it is:
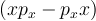 . In order to work this out it is helpful to apply the operator to a test function.
. In order to work this out it is helpful to apply the operator to a test function.
![[x,p_x] f(x) = (x p_x - p_x x)f(x) = (x (-i \hbar d/dx)) f(x) - ((-i \hbar d/dx) x) f(x)](/csm/wiki/images/math/d/9/2/d92856a7dfa08740e07ca92020ad4146.png)